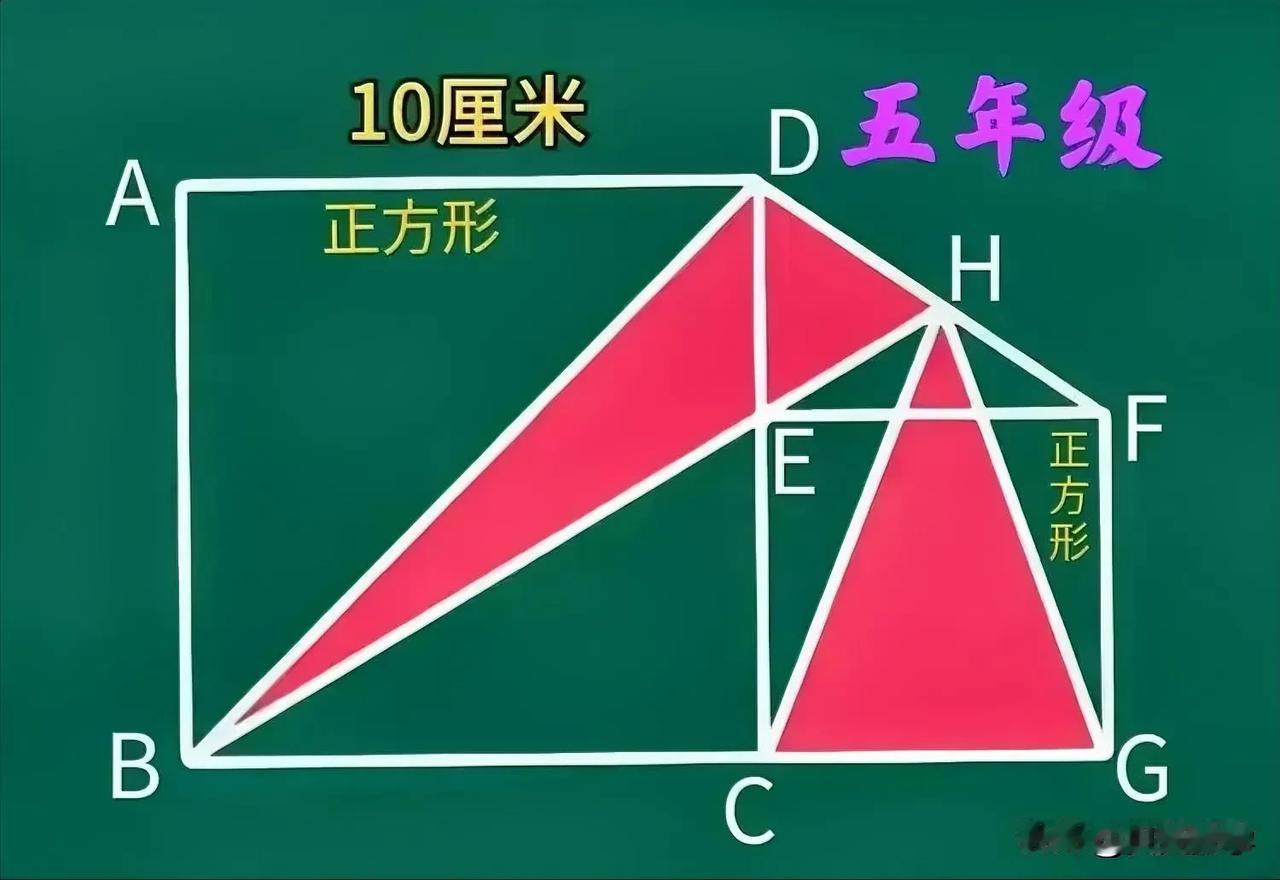
“几乎全军覆没,个别尖子生除外!”有家长利用平方差公式秒解,但孩子听不懂!限用小学知识,如何求解?这是一道小学三年级数学竞赛题:两正方形边长之差、面积之差均已知,但边长均未知,求其各自的面积! 如图,一大一小两正方形并排摆放在一起,其边长差为4,面积差为96,这两个正方形面积各为多少? —————————— 提示一:翻折图形(或将小正方形放入大正方形一角)+先小正方形边长,适合三年级! ①将小正方形沿CE翻折至大正方形内,翻折后的小正方形记为CEF'G'。 ②延长FE与AB相交于点M,延长G'F'与AD相交于点M,则AMF'N为正方形,其面积为16。 ③BG'F'M与DEF'N均为长方形,且长宽分别相等(宽均为4),故其面积相等、均为(96-16)÷2=40,从而其长为40÷4=10,也即小正方形的边长10,大正方形边长为14。 提示二:图形翻折、不求小正方形边长,适合五、六年级! ①同于提示一,可知S正方形AMF'N=16,S长方形BMF'G'=S长方形DNF'E=40。 ②由“共边长方形面积之比等于另一边边长之比”可得,AMF'N/S长方形BMF'G'=NF'/F'G'=S长方形DNF'E/S正方形CEF'G',从而S正方形CEFG=40×40÷16=100。 提示三:平方差公式,适合初中生! 大小正方形的边长分别记为a和b,则有a-b=4,a²-b²=96,由平方差公式可得a+b=24,从而求得a=14,b=4。 友友们,怎么看?欢迎留言分享! 妙笔生花创作挑战 小学数学
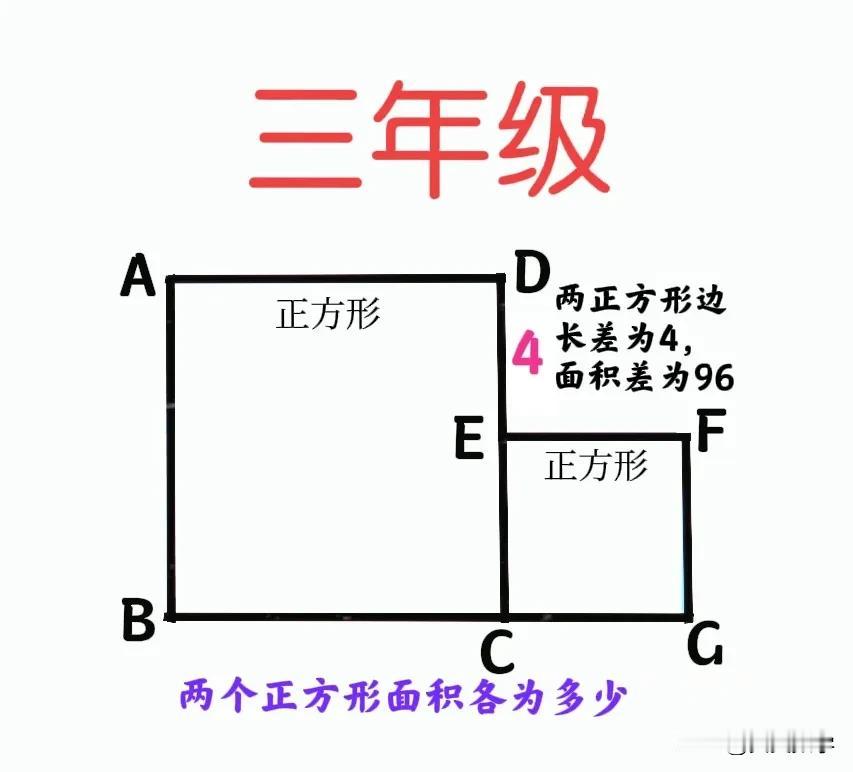
设小正方形边长为x,则2*(4*x)+4*4=96,则x=10,小正方形边长为10,大正方形边长14
把小正方形往大正方形里折,未重叠部分既为面积差96。未重叠部分正好就是两个宽为4,长为大正方形边长a的长方形面积,减去两长方形重叠部分边长为4的小正方形面积。既2*4a-16=96.a=14(答题得写画辅助线过程)


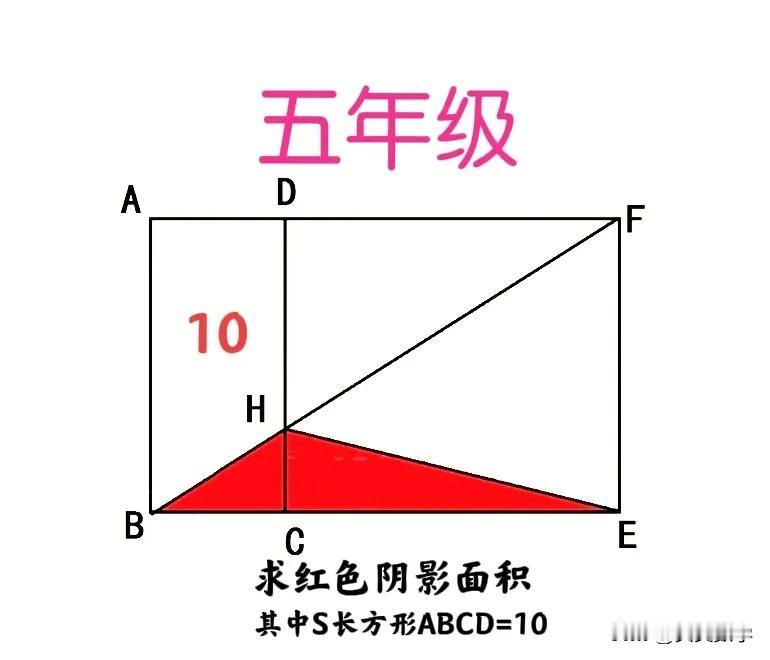


云南白药
圆规以D为原因,DE为半径,在AD上找到点H,延长FE交AB于J,过点H做DC平行线交BC于I。此时正方形EFGC=正方形JKIB,正方形HDEK面积=16,得出长方形AHKJ面积=长方形IKEC面积=(96-16)÷2=40,得出AH=EC=10,AD=DC=14。正方形ABCD面积=14×14=196。正方形EFGC面积=10×10=100
正在输入 回复 01-06 21:17
三年级哪有这么复杂
开遍天下无敌手
现在都不背20以内平方数了吗?
亚楼
解:设小正方形边长为a,依题意,(a+4)²-a²=96,(2a+4)*4=96,a=10,a+4=14,10²=100,14²=196即小正方形边长面积是100,大正方形面积是196。
Locky
看图找方程而已
用户14xxx27
大14,小10
果子狸
3年级,没有学未知数,没有学圆
云南白药
圆规以D为圆心,DE为半径,在AD上找到点H,延长FE交AB于J,过点H做DC平行线交BC于I。此时正方形EFGC=正方形JKIB,正方形HDEK面积=16,得出长方形AHKJ面积=长方形IKEC面积=(96-16)÷2=40,得出AH=EC=10,AD=DC=14。正方形ABCD面积=14×14=196。正方形EFGC面积=10×10=100
九月
把小正方形放里面,