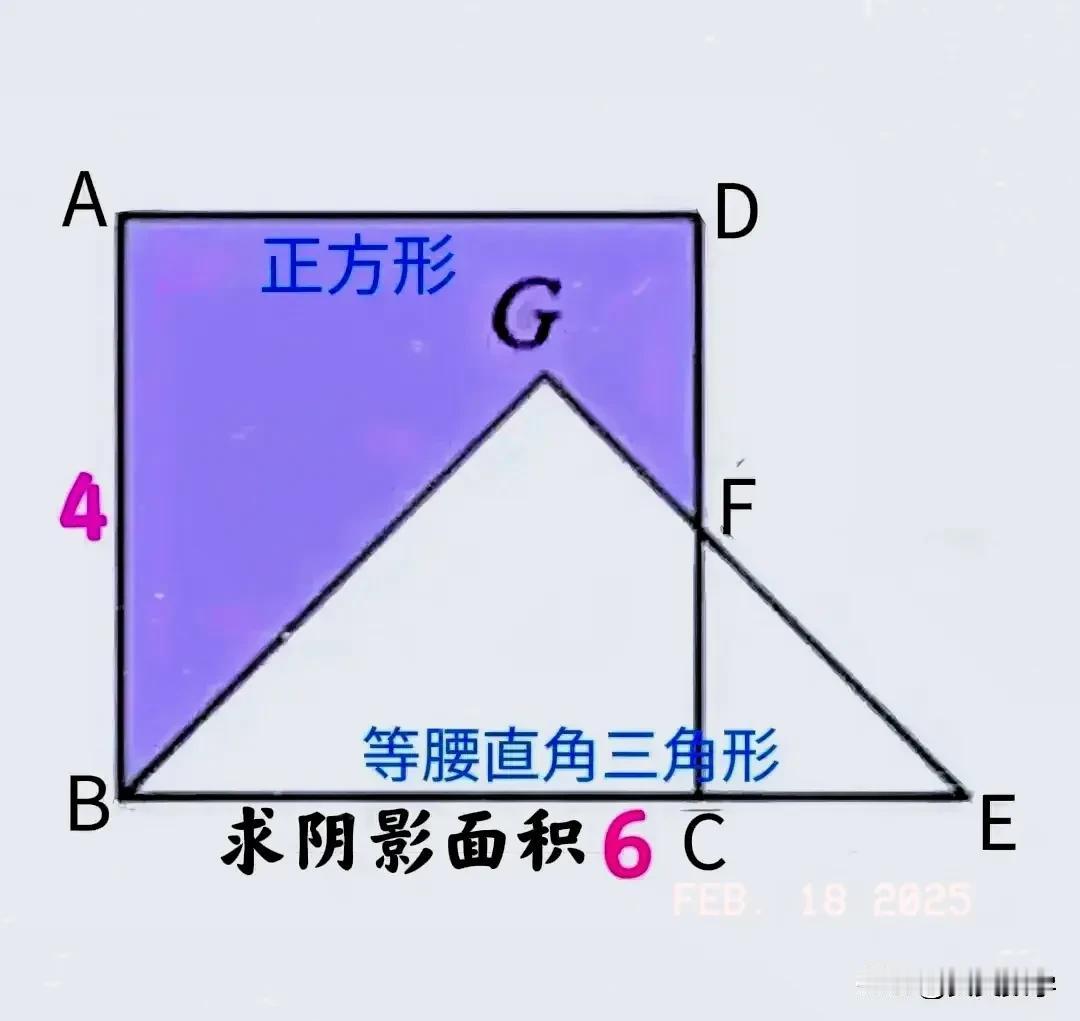
“会者不难，难者不会！”小学五年级数学拓展题型：如何借助面积差、求不规则图形面积

“会者不难，难者不会！”小学五年级数学拓展题型：如何借助面积差、求不规则图形面积？仅斜边已知，咋求等腰直角三角形面积？ 如图，正方形ABCD边长为4，点E在BC的延长线上且BE=6，以BE为斜边作一等腰直角三角形BEG，EG与CD相交于点F，求阴影面积。 解题关键：找出隐含条件，由△BCG为等腰直角三角形，易知△CEF也为等腰直角三角形！ ———————————— 提示：等腰直角三角形面积等于斜边平方的1/4（即4个相同的等腰直角三角形可拼成1个以斜边为边长的正方形）！ ①S△BEG=6×6÷4=9。 ②CF=CE=6-4=2，故S△CEF=2×2÷2=2，从而S四边形BCFG=9-2=7，因此S阴影=16-7=9。 ———————————— 这种通过面积差来求不规则图形面积的方法在小学数学中是非常重要的。它不仅考验孩子们对图形的观察能力，还考验他们对特殊三角形面积公式的运用能力。 理解等腰直角三角形面积等于斜边平方的1/4这个公式的由来很有趣。我们可以这样想，等腰直角三角形如果以斜边为边长构建一个正方形，这个正方形正好可以分割成4个完全相同的等腰直角三角形。这就像一个拼图游戏，规则图形和不规则图形之间通过这样巧妙的关系联系起来。 对于这道具体的题目而言，从已知条件到一步步求出阴影部分面积，每一步都蕴含着逻辑推理。在求出S△BEG和S△CEF之后，通过减法得出S四边形BCFG的面积，这一步是解题的关键环节。它就像是一座桥梁，连接着正方形的面积和阴影部分的面积。 这种题型还可以有很多的变形。比如改变正方形的边长，改变等腰直角三角形的斜边长度，或者增加更多的图形元素，使图形变得更加复杂。但不管如何变形，核心的解题思路都是类似的。那就是找到规则图形与不规则图形之间的面积关系，通过已知的条件逐步求出所求图形的面积。提醒孩子们在学习数学的过程中，要注重对基本概念和公式的理解。 家长和老师在辅导孩子做这种题目的时候，可以引导孩子自己去发现图形中的隐含条件。像这道题中的隐含条件，如果孩子自己能够发现并理解，那么对于解题会有很大的帮助。这样可以培养孩子的自主学习能力和逻辑思维能力，而不仅仅是让孩子记住解题的步骤。这对于孩子在数学学习的长远道路上，是有很大益处的。 友友们，怎么看？欢迎留言分享！