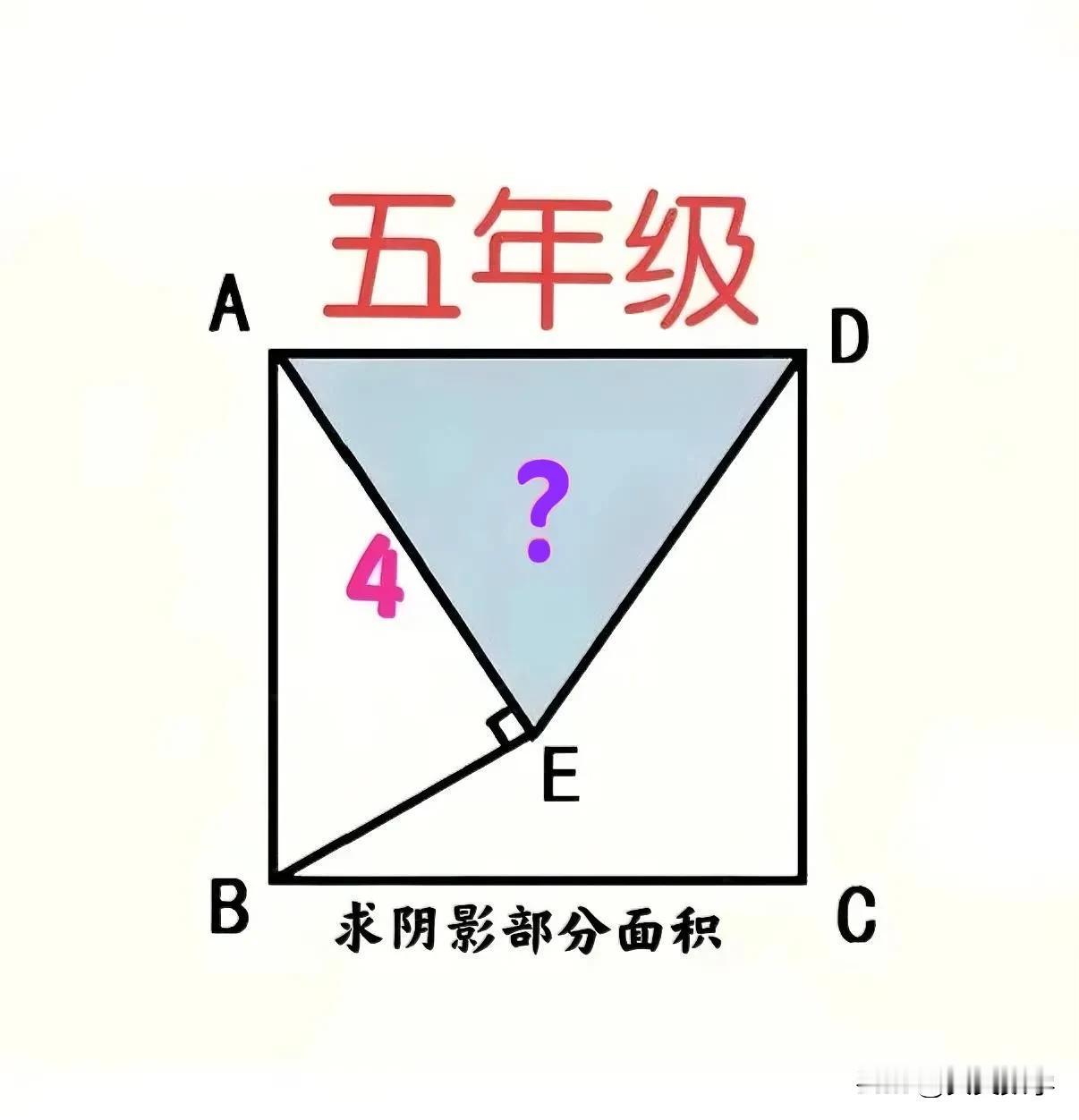
“全年级200多人，会做的不到10人！”这是一道海口市某私立小学五年级数学竞赛附加题：难度很大！三角形仅一边已知，咋求其面积？ 如图，E为正方形ABCD内一点，连接AE，BE和DE，ABE为直角三角形，AE=4，求阴影部分三角形ADE的面积。 ————————— 个别孩子这样做：特殊情形法！适合填空或选择题 考虑特殊情形：E为正方形的中心，即E在BD上。此时△ABE和△ADE均为等腰直角三角形，其面积均为4×4÷2=8。 但作为计算题，被老师扣了不少分！ 个别培优的孩子这样做：赋值+简单勾股数+弦图！适合填空题或选择题 ①假定正方形边长为5，则由简单勾股数可知BE=3。 ②作弦图，可知△ADE底边AE上的高也为4，从而S△ADE=4×4÷2=8。 个别超前学习的孩子这样做：三角形全等！适合初中生 过点D作AE上的高DF，则△ADF≌△ABE，故DF=AE=4，从而S△ADE=4×4÷2=8。 学霸这样做：图形旋转！适合五年级 ①将△ABE绕点A逆时针旋转90°至AB与AD重合，旋转后的三角形记为△ADE'。 ②注意到∠EAE'=90°，∠AE'D=∠AEB=90°，故AEDE'为直角梯形，即AE⫽DE'。 ③注意到AE'=AE=4，由同底等高三角形面积相等可知，S△ADE=S等腰直角△AEE'=4×4÷2=8。 友友们，怎么看？欢迎留言分享！ 妙笔生花创作挑战