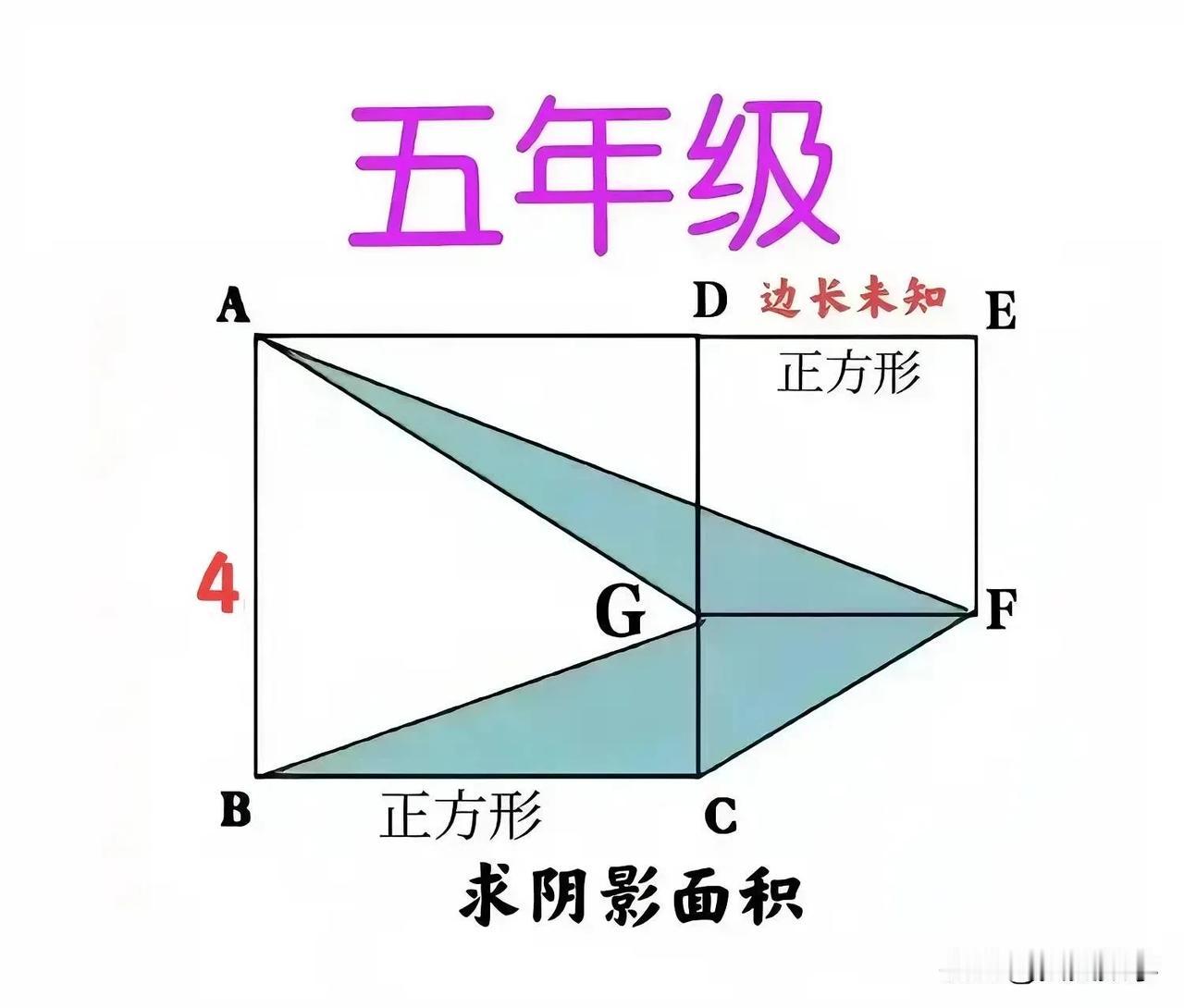
“正确率不足5%!”大量同学被“难”住的原因找到了,只因正方形DEFG的边长未知!这是一道小学五年级数学同步训练“拓展题”:仅一边已知,咋求不规则图形面积? 如图,两个正方形ABCD和DEFG,其中一个边长为4,另一个边长未知,求阴影部分面积。 ————————— 提示:连接DF! ①同底等高三角形面积相等,故S△AFG=S△DFG,从而S△AFG+S△CFG=S△CDF。 ②注意到AD=CD,FG=DG,故△ADG与△CDF等底等高,从而S△ADG=S△CDF。 ③S阴影=S△ADG+S△CDG=1/2S正方形ABCD。 友友们,怎么看?欢迎留言分享! 小学数学 妙笔生花创作挑战
那么复杂干嘛,令小正方形边长为一个小于大正方形边长的具体数值计算,如令小正方形边长等于大正方形边长的一半等于2,(2*2+2*2+4*2)/2,阴影部分面积为8,这样的题,就要这样搞

胖朗朗
连接AC和DF,有S△ACG=S△BCG,又因AC∥DF,所以S△ACF=S△ACD=4×4÷2=8。
我的UC
易知,三角形AGF面积等于三角形DGF,也等于三角形DEG,都是小正方形一半。把三角形CGF等高变形,F点拉到E点,右边部分合起来就是三角形CDE。把三角形CDE绕D点顺时针转90°,就和三角形ADG重合。所以阴影面积就是大正方形一半4×4/2=8
用户10xxx42 回复 12-25 19:47
答案都写错,AGF变型为DGF,CDF变型为CDE.
我的UC 回复 用户10xxx42 12-26 11:24
没懂多看看
用户56xxx87
8,方程法
Locky
连结df,bd替换等面积的图形,就清晰了。
用户10xxx48
8
孤独着
做个答案还写错,零分,