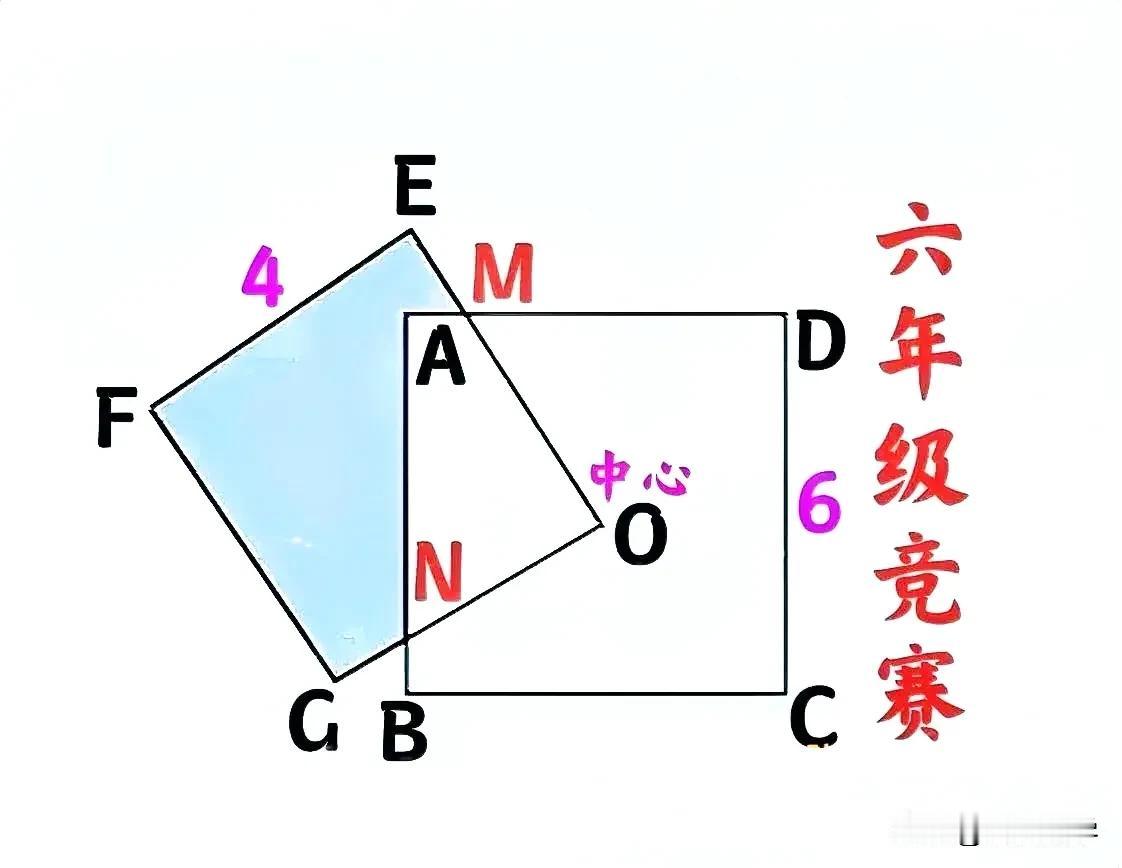
“几乎团灭，极个别尖子生除外！”有不少家长认为题目超纲了，示意图不规范！对几何直观能力特别强的孩子来说，几乎是送分！这是一道小学六年级数学竞赛题： 两个正方形的边长分别为4和6，小正方形的1个顶点与大正方形的中心重合，求小正方形去掉与大正方重合部分后的剩余图形面积。 ————————— 有人这样做，方法①：三角形全等，适合初中生！ 如图，连接OA和OB，则△OAM≌△OBN，故S四边形AMON=S△AOB=1/4S正ABCD，从而S阴影=S正OEFG-1/4S正ABCD=16-36/4=7。 也有人这样做，方法②图形旋转+特殊情形，适合小学生！ 将小正方形OEFG绕点O旋转至OM垂直AD、ON垂直AB，此时四边形AMON为正方形，其面积为1/4S正ABCD。同于第一种方法，求得阴影部分面积为7。 还有人这样做，方法③图形旋转+面积不变！ 小正方形OEFG绕点O旋转过程中，四边形AMON的面积为定值，恒等于1/4S正ABCD=9，故阴影部分面积恒为16-9=7。 也有人对方法③提出质疑：小正方形OEFG绕点O旋转过程中，四边形AMON的面积并非定值！ 比如当小正方形OEFG旋转至OE过点A、OG过点B时，由于OE=4＜3√2=OA，此时点E和G均落入大正方形ABCD内，小正方形的边EF和FG均与AB相交，记其交点分别为点P和点Q，则PQ=AB-AP-BQ=6-2×(6-4√2)=8√2-6，从而S阴影=S△FPQ=(4√2-3)²=41-24√2＞7。 友友们，怎么看？欢迎留言分享！ #小学数学# #妙笔生花创作挑战#