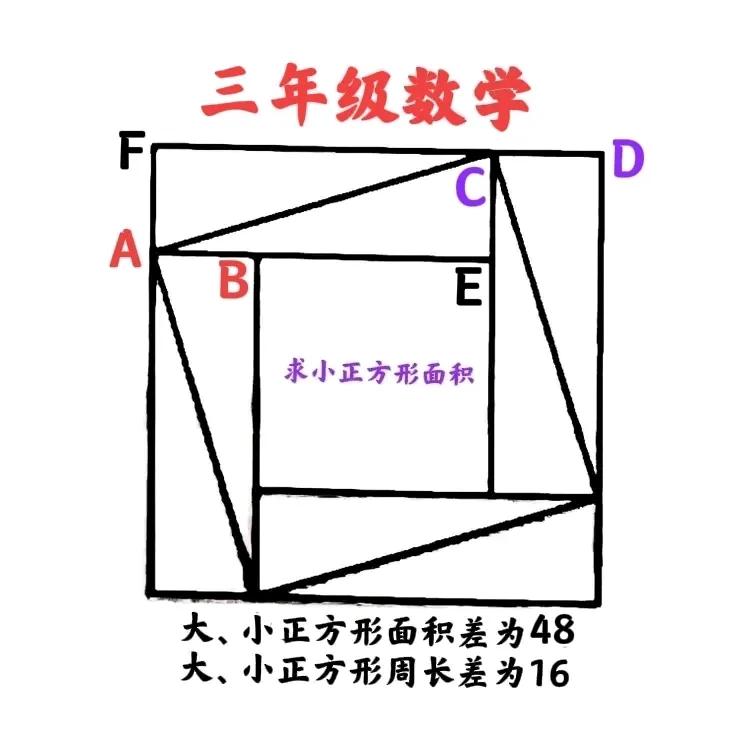
“团灭，一个不剩！”这是一道小学三年级数学竞赛题： 如图，有大、中、小三个正方形，大、小两正方形面积之差为48、周长之差为16，求小正方形面积。 有人说，超纲了！非使用平方差公式和解方程不可！设大小正方形边长分别为a、b，由大面积差可得a²-b²=48，由周长差可得(a-b)×4=16即a-b=4，从而由平方差公式可得48=(a+b)(a-b)=4(a+b)也即a+b=12，故a=8，b=4！ 有人说，简单！数形结合秒解！注意到AB=CD=DE，由面积差可得S长方形AECF=48÷4=12，由周长可得8AB=16也即AB=2，从而求得AE=6也即BE=4！ 友友们，怎么看？有啥想法或思路，欢迎留言分享！ #小学数学#