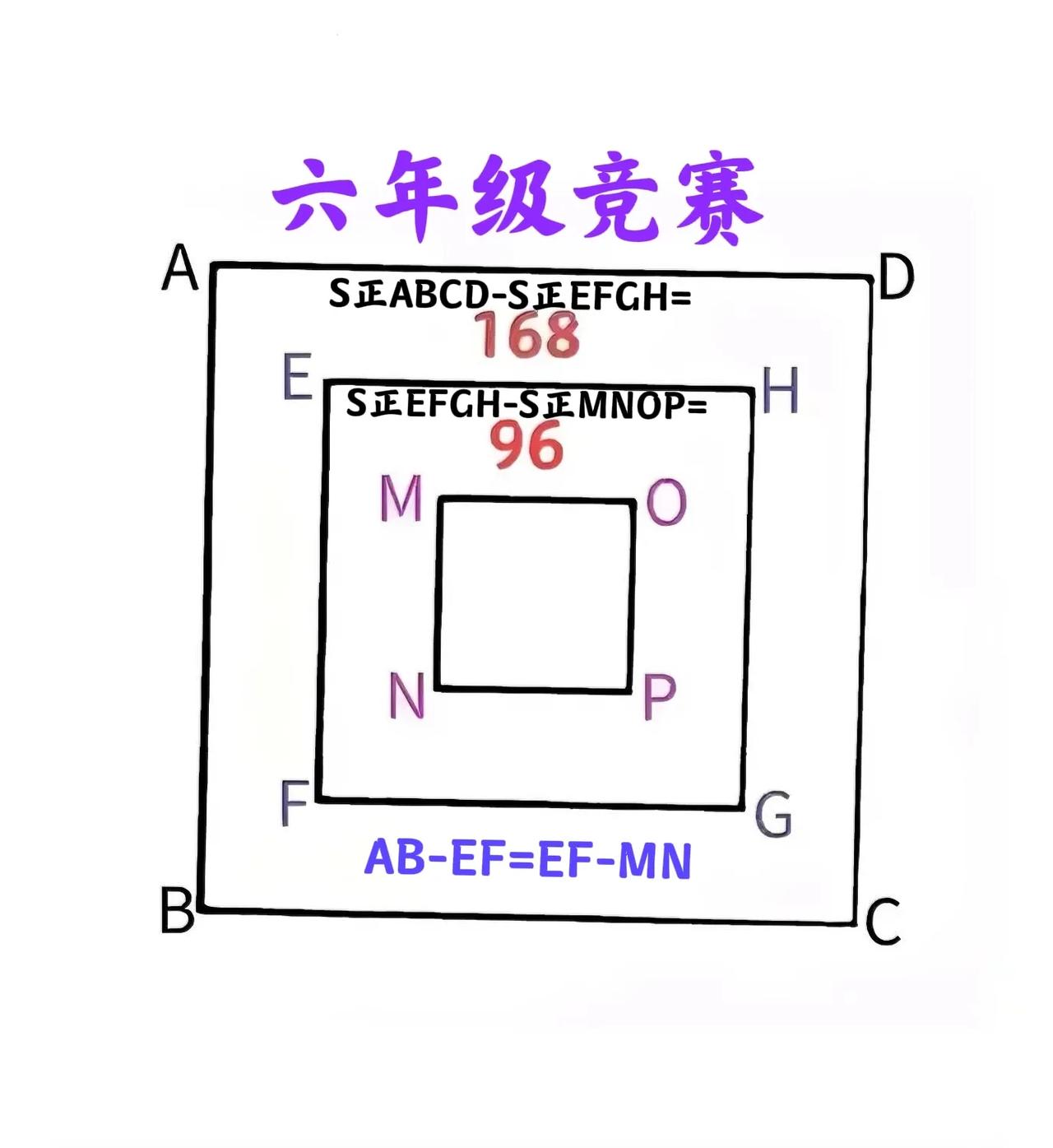
“超难！全军覆没！”有人说超纲了，非使用平方差公式不可！这是一道小学六年级数学竞赛题：三个正方形的面积差已知、边长等差，咋求其面积？ 如图，大中小三个正方形ABCD、EFGH的MNPO，大正方形与中正方形面积差为168，中正方形与小正方形面积差为96，三个正方形边长等差（即大正方形与中正方形边长之差、等于中正方形与小正方形面积之差），求大正方形ABCD的面积。 提示：将三个正方形重新摆放至其中心重合即A、E、M、P和C五点共线！①连接AEMPC和BFNOD，则ADHE和EHOM均为等腰梯形，且底角均为45°。②过点M作AD和EH的垂线MK和ML，过点E作AD的垂线EJ，由三个正方形边长等差可知EJKL为正方形。③S△AEJ=S△EML，故（168-96）÷4=S梯形ADHE-S梯形EHOM=2S正方形EJKL，即S正方形EJKL=9，从而AJ=EJ=EL=JK=ML=3。④由S梯形EHOM=24及ML=3，可求得MO=5。 友友们，怎么看？有啥想法或思路，欢迎留言分享！ #小学数学#
使A、E、M点重合，AB、EF、MN共线，AD、EH、MO共线，延长FG交DC于点I，延长OP分别交FG、BC于点J、K，设AB-EF=EF-MN=d，则长方形IJKC长为2d，宽为d（或其为两个边长为d的正方形组成），面积2d*d=168-96，可得d=6;设小长方形边长为a,则a*6+(a+6)*6=96，a=5；正方形ABCD边长为5+6+6=17，面积为17²
移动内部的两个正方形，将三个正方形左下角重叠，这样画图都可以求出大正方形的面积
太难