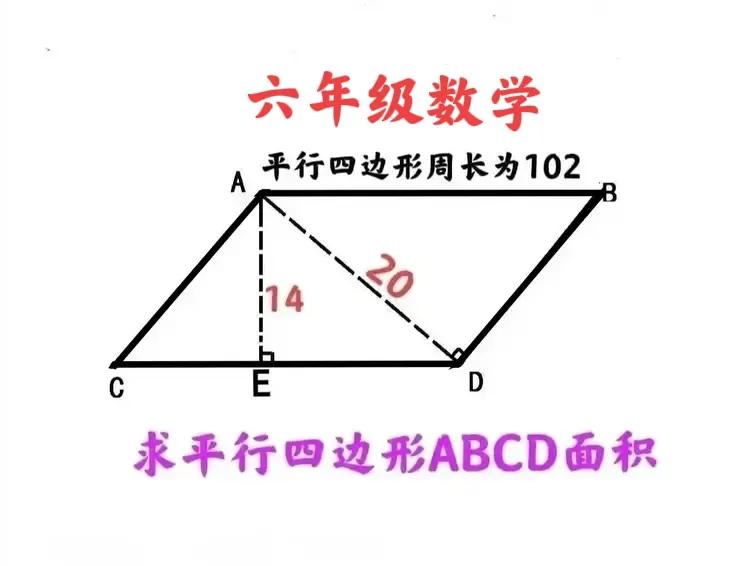
“团灭实属必然,只因此题无解!”这是一道小学六年级数学题:平行四边形边长未知,咋求其面积? 如图,平行四边形ABCD的周长为102,AE垂直CD且AE=14,AD垂直BD且AD=20,求平行四边形ABCD的面积。 有人说,由S△ACD=S△ABD可得14×CD=20×BD即CD:BD=10:7,再由BD+CD=51可知CD=30,BD=21,从而S平行四边形ABCD=14×30=420。 有人说,由20²+21²≠30²可知△ABD并非直角三角形,故条件矛盾,此题无解! 友友们,怎么看?有啥思路或想法,欢迎留言分享! #小学数学#

喂,是你
ab+db=51 ab*14=bd*20 ab*14=(51-ab)*20 14ab=1020-20ab 34ab=1020 ab=30 bd=21 30*14=21*20=420
喂,是你 回复 06-21 00:40
ad+bd=51 ab²-bd²=(ab+bd)(ab-bd)=20² ∴ab-bd=400/51 ∴
我入地狱[已注销]
△AED∽△CAD,再带入AE,AD值,得到CD=200/√51。所以是数值出错了。
杨百万在线
直接方法,长为A,宽为B,2A+2B=102,1/2 *A*14=1/2 *B*20,7A=10B,17A=510,A=510/17,长方形面积=14A=14*510/17
M丶H 回复 06-24 12:39
长方形属于平行四边形,平行四边形不等于长方形。扣分。
用户12xxx76 回复 M丶H 09-06 14:55
本题中,三角形移一下就是长方形,在本题中没毛病。
血滴子
x=30
血滴子
14x=20(51-x)
血滴子
设cd为x,则 bd为51-x
摩客小志
条件多给了一个,这样题目自身就矛盾了