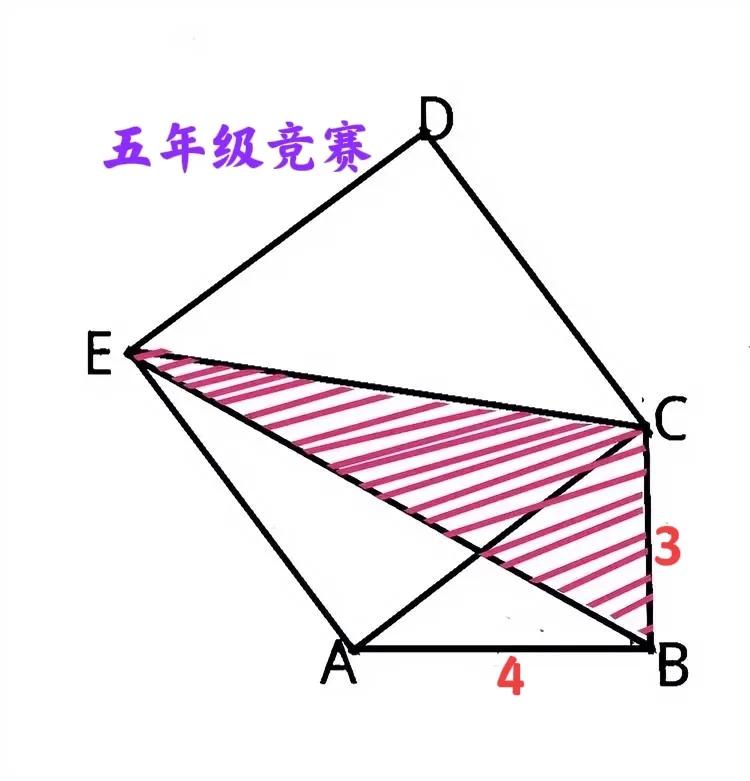
#小学数学# “几乎全军覆没，个别学霸除外！”这是一道小学五年级数学竞赛题：三角形仅一边已知，咋求其面积？ 如图，ACDE为正方形，以AC为斜边作一直角三角形ABC，AB=4，BC=3，求红色阴影三角形BCE的面积。 难点：如何求△BCE底边BC上的高！ 有人说超纲了，需使用勾股定理和三角形全等！①使用简单勾股数或勾股定理可求得正方形ACDE的边长为5。②过点E作BA延长线的垂线EF，则△AEF与△ACB全等，故AF=3，从而△BCE底边BC上的高恰好等于BF=7。 有人说没超纲，将②中△AEF绕点A顺时针旋转90°至AE与AC重合，旋转后的三角形记为ACF'，则ABCF'为一长方形，从而AF=AF'=BC=3。 友友们，怎么看？有啥思路和看法，欢迎留言分享！
正方形面积+ABC面积-CDE面积-ABE面积，计算方法上面都解释的很清楚了。
以AE为斜边，作△EB'A=△ABC，B'A=BC=3，B'B=7，连接B'C，∠EB'A=90°，∠ABC=90°，则EB'∥CB，S阴=S直角△B'BC=1/2*BC*BB'=10.5
延长BA，过E点BA延长线的垂直线EF。∠a+∠c=∠b+∠c，∠a=∠b。根据相似三角形等边比可以得出AE/AC=1=AF/3,则AF=3，S△BCE=3×7÷2=10.5
10.5