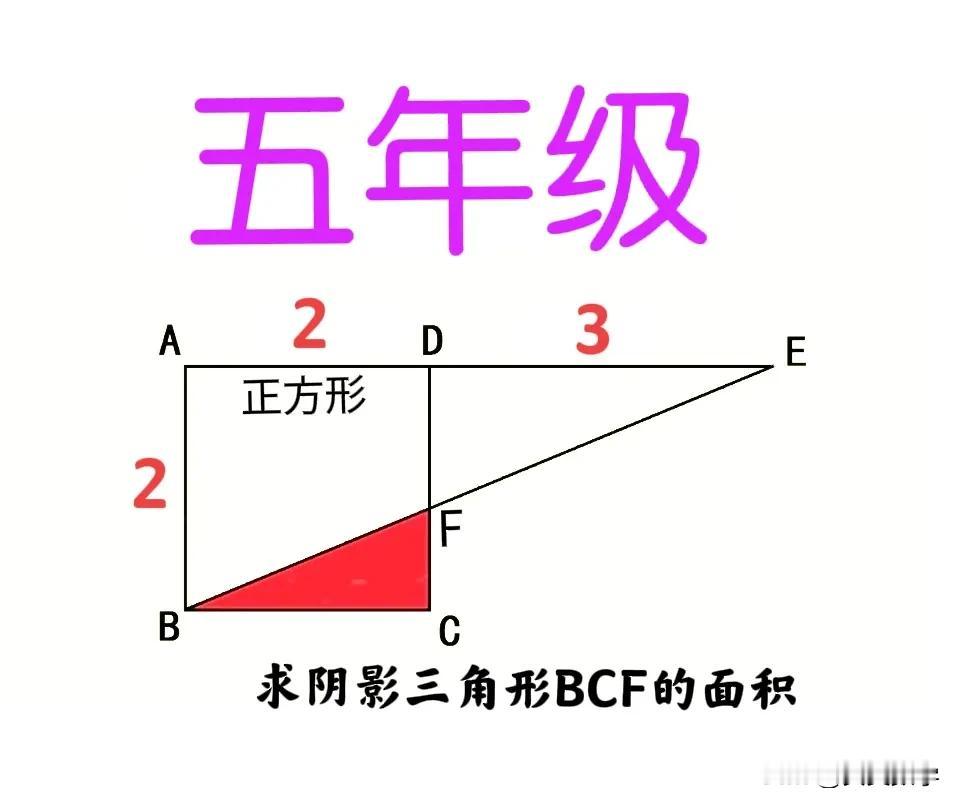
“几乎团灭，个别尖子生除外！”正确率极低的原因找到了：绝大多数孩子、不知如何求直角边CF的长！这是一道小学五年级数学竞赛附加题：仅一直角边已知，另一直角边及斜边均未知，咋求面积？ 如图，正方形ABCD的边长为2，延长AD至点E使得DE=3，BE与CD相交于点F，求阴影三角形BCF的面积。 ———————— 提示一：同底等高三角形面积性质，并求CF，适合五年级！ ①连接AF、BD和CE，则S△ADF=S△BDF，从而S△AEF=S△BDE=S△CDE=DE×CD÷2=3。 ②DF=2S△AEF÷AE=6÷5=1.2，故CF=2-1.2=0.8，从而S△BCF=2×0.8÷2=0.8。 提示二：等高三角形面积比等于底边之比，不求CF，适合六年级！ ①连接BD和CE，则S△BDE=S△CDE=3，S△BCE=S△BCD=2。 ②S△BDF/S△BCF=DF/CF=S△DEF/S△CEF，故DF/CF=S△BDE/S△BCE=3/2，从而S△BCF=1/5S正方形ABCD=0.8。 提示三：三角形相似或平行线段比，适合初中生！ DF/CF=DE/BC=3/2，余下同于“提示二”。 友友们，怎么看？欢迎留言分享！ 小学数学