微分流形（differentiable manifold）也称为光滑流形，是带有微分结构的拓扑流形。它是一个Hausdorff空间，对于任意点x∈M，存在x的邻域U，使得U同胚于Rm的一个开集。

通过坐标卡（U,φU）可以定义M上点的局部坐标。为了使坐标卡之间能够相容，需要满足一定的条件，即坐标变换函数在重叠部分是光滑的。

设M是一个豪斯多夫空间。U是M的开集,h是U到n维欧氏空间R的开集(常取为单位球内部或立方体内部等等)上的一个同胚映射,则(U，h)称为一个坐标图，U称为其中点的一个坐标邻域。设M为开集系{Uα}所覆盖,则(Uα,hα)的集合称为M的一个坐标图册。如果M的坐标图册中任何两个坐标图都是C相关的(坐标图册应该是极大的，即若任一坐标图与坐标图册中每一个坐标图都相容则其自身也属于坐标图册),则称M有C微分结构,又称M为n维的C微分流形。

那么，定义微分流形这个概念是为了解决什么问题呢？

B站上有一位老师对这个问题讲述得很好，这里简述如下：

定积分的求解过程我们都知道，就是一条曲线用一个函数f(x)表示，然后求出面积：

那如果一条曲线太复杂，无法用同一个函数表示出来的时候怎么办呢？

如下图：

将这条曲线划分为不同的区间，每个区间对应于直线上的一个开区间：

相交部分存在如下关系：

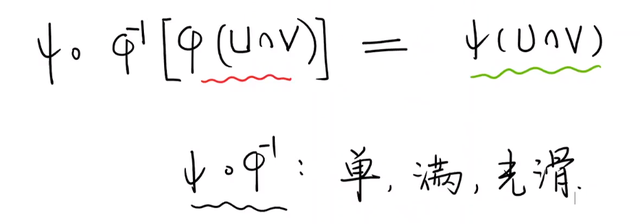
同样，对于二维空间：

经过这样处理以后，微分流形上可以定义可微函数、切向量、切向量场、各种张量场等对象，并可以赋予更复杂的几何结构以研究它们的性质。