切向量场定义的意义在于描述流形上每一点处的切向量，并且这些切向量随着基点的连续移动而连续变化，为微分流形理论提供了基础。

详细来说，设M是一个可微的流形，切向量场就是在M的每一点处都安放一个切向量。这些切向量不是孤立存在的，而是要求当它们的基点在流形上连续移动时，它们也跟着连续地变动。这种描述方式使得我们能够在流形上全局地研究切向量的性质和行为。

在微分几何中，切向量场可以看作是流形上的向量场，它们都可以看作是从空间到空间的映射。这种映射关系使得我们能够利用向量场的性质来研究切向量场的性质，进一步丰富了微分流形理论的内容。

切向量场与方向导数存在密切关系，这里先介绍一下方向导数的概念：

在 n 维欧氏空间上，取一个 n 元光滑函数 f, 它在方向 v 上的方向导数可以表示为

其中 vi 是 v 的分量。这是一个向量函数，在 Rn 上具有表达式

将上式与方向导数的定义相对比，可以看出两者之间具有相同的意义。

因此也可以认为

称 d/dv 是 Rn 上的一个切向量场。

现假设 光滑流形

构造集合

这里的TpM代表点p的所有切向量的集合。

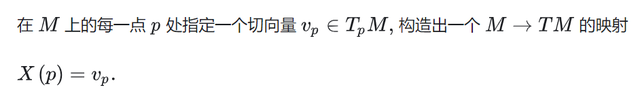
再假设U为M上的开集，在M的每一点p处：

如果

切向量场的概念在微分流形理论中占据重要地位。一方面，它是研究流形局部性质的重要工具，通过切向量场可以研究流形在某一点处的切线方向、曲率等几何性质。另一方面，切向量场也是连接拓扑和几何的桥梁，为研究流形的整体性质提供了有力手段。