分享数学的技巧，分享数学的乐趣。

今天专题分享初中数学两个最重要的数学模型，将军饮马和一箭穿心。很多题目中这两个模型都会碰面，从将军一马到一箭穿心，完美的模型组合。

途虫精讲初中数学模型

纯手写版教案来了，很多人说喜欢，我也不吝啬，尽可能跟大家分享。

将军饮马模型大家都很熟悉了，先重点给大家讲讲一箭穿心模型，一箭穿心最值模型经常跟隐圆模型相伴而行，隐圆模型也叫辅助圆模型，初中常考的隐圆模型有四种款式，我给你总结出来了。

初中数学隐圆模型的四种款式

定点定长，定弦定脚，对角互补，这是出现频率最高的三种隐圆模型，最主要是用来确定动件的运动轨迹。将军饮马动点的轨迹是直线形，隐圆模型的动点是孤线型。

一箭穿心最值模型

好了，我们来了解一下一箭穿心，很简单，它主要是来解决圆外一点到圆周上某一点距离的最大值和最小值的问题。无论是最大值还是最小值，都必须穿过圆心，远端是最大值，近端是最小值，看上面图形就明白了。

光说不练等于白干，当然要通过题目来加深记忆和巩固知识，精心挑选了三道题，真的都是非常好的题目。

精选题目一

第一道题目只有隐圆模型和一箭穿心，特别注意求一定一动线段的最值，通常先找出动点的运动轨迹。因为角APB=90度，所以P点的运动轨迹是一个圆，这是定弦定角款，然后就可以套用一箭穿心模型，连接D点和圆心O就可以了，非常的快捷。

精选题目二

这一道题可以说是将军饮马和一箭穿心两个模型的完美结合，我已经发了专门的解题视频，大家可以查看我前段时间发的视频。经典版的将军马是两定一动，而这一道题P点和G点都是动点，那么怎么办呢？我们可以先假设G点是定点，那么PA+PG就是将军饮马模型，所以先做A点关于BC的对称点A撇点，但因为G点的运动轨迹是一个圆，所以除了满足将军饮马以外，还得满足一箭穿心，这样才能求出PA+PG的最小值。

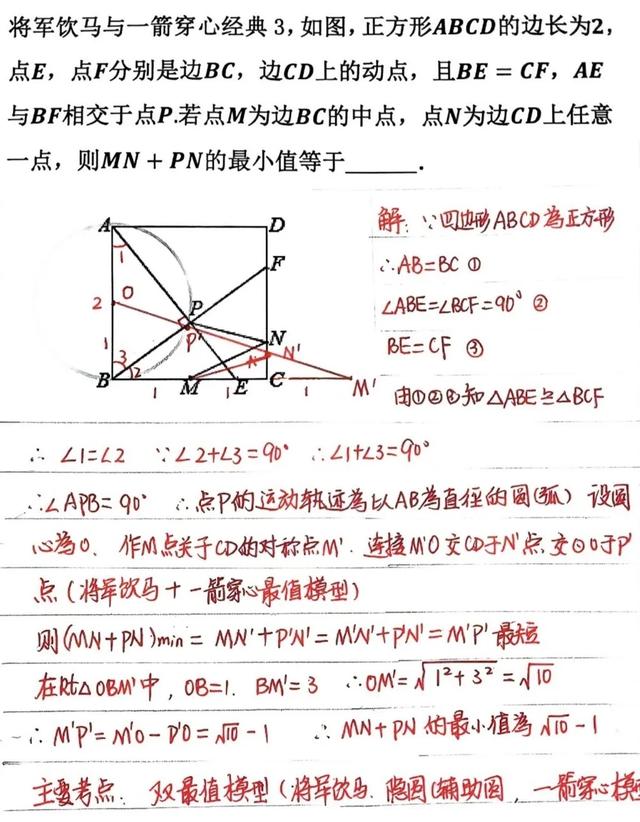
经典题目，第三题

第三题跟第二题的思路是差不多的，都是将军饮马+一箭穿心，我就不再重复啰嗦了。这道题我也已经发过讲题视频，大家可以去查看。

这就是将军饮马和一箭穿心的完美结合，更多途虫数学的手写教案，敬请期待。