泛函的变分在数学中有着广泛的应用和重要的意义,它不仅是微积分的一个自然扩展,还是许多数学分支的基础。
首先,泛函的变分扩展了微积分的研究范围,使其能够研究更复杂的函数类,例如无限维空间中的极值问题和最优控制问题等。
其次,泛函的变分理论在偏微分方程、概率论等多个数学分支中都发挥着基础性的作用。在概率论中,我们也经常需要找到一个随机变量的概率分布,使得某种期望值最大或最小,这个期望值也是通过泛函的变分来定义的。
此外,泛函的变分还为我们提供了一种强大的工具,即变分法。变分法是一种寻找函数的极值或最优解的方法,它通过求解欧拉-拉格朗日方程来找到使泛函取得极值的函数。
泛函的变分不仅是数学研究中的一个重要概念,而且在实际应用中也具有广泛的价值和意义。
如同函数的微分是增量的线性主部一样,泛函的变分是泛函增量的线性主部。作为泛函的自变量,函数x(t)在x0(t)的增量记为

也称函数的变分。由它引起的泛函的增量记作





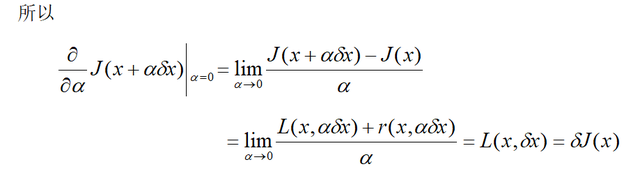
对照网络一篇文章的说明:

这里



以下是关于泛函极值的变分表示定理:



再由(4)式,便可得到(5)式。


习惯一个人
一个很奇妙案例供大家参考。 陀螺仪在当今社会应用很广,陀螺仪其中一个基本特性:定轴性,当陀螺转子以高速旋转时,在没有任何外力矩作用在陀螺仪上时,陀螺仪的自转轴在惯性空间中的指向保持稳定不变,即指向一个固定的方向;同时反抗任何改变转子轴向的力量。这种物理现象称为陀螺仪的定轴性或稳定性。其实以上的基本特性描述是不严谨的,以上的基本特性描述是只有在转子轴向在大于0度小于90度范围内才可以成立的,在大于等于90度小于180度范围内是不成立的,在夹角等于90度时反抗任何改变转子轴向的力量大小和方向无法确定(有点像薛定谔的猫),当夹角稍微大于90度时反抗任何改变转子轴向的力量大小和方向确定,不在是保持陀螺仪的自转轴在惯性空间中的指向保持稳定不变,而是指向一个固定的相反方向,明显可以重复观察到,网上有卖金属倒立自动翻转陀螺可供参考,是最典型的实践证据。自动翻转陀螺在翻转的同时重心增高,势能变大,传统物理学理论无解。 陀螺仪的定轴性,在反抗任何改变转子轴向过程中如果不存在重力以外的外力,定轴性表现是和轴向角动量守恒是冲突的。研究结果可以理论个实验重新定义 时间 和 空间。