在黎曼几何中，每一点建立不同的局部坐标系是为了描述流形上各点附近的几何性质，并考虑坐标系之间物理量的变换。

由于流形上不同位置的几何性质可能不同，因此需要在每一点都建立局域的坐标系来准确描述该点附近的几何特征。同时，这些局部坐标系之间的关联通过全局的参数来描述，从而能够全面反映流形的整体结构。

比如，一架飞机从中国飞到美国，经过中国某位置时，测得一个速度p，到了美国某位置时，测得同样的速度也是p，但两者的局部坐标系肯定是不一样的。因此，需要将一个坐标系中的向量(美国速度p)，变换到另外一个位置的坐标中(中国坐标系)去，才能真正对两个向量进行比较。

考虑两个位置x和x+dx的变换，即怎么将位于x+dx处测量的向量A（x+dx处有自己的坐标系），用x处的坐标系表示出来。这用到一个变换矩阵。

以下内容来自网络。

已知测地线方程为：

改写为：

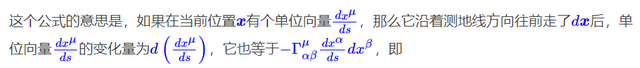
意思就是左边的向量变成了右边的向量。

从x到x+dx的坐标变换矩阵就为

这样，如果反过来，从x+dx到x的坐标变换矩阵就为

所以，克里斯托费尔符号

就把x到x+dx的坐标联系了起来，因此称为联络系数。