密切平面、从切平面和法平面是微分几何中描述曲线在某点附近几何性质的重要平面。

密切平面：

定义：过空间曲线上P点和曲线上与P点充分靠近的点Q，可作一平面σ。当Q点沿着曲线趋近于P时，平面σ的极限位置π称为曲线在P点的密切平面。

密切平面是曲线在某点处最“贴近”的平面，它反映了曲线在该点附近的弯曲情况。

从切平面：

从切平面是与密切平面垂直的平面。

法平面：

法平面是垂直于曲线在某点的切线的平面。

法平面与切平面（包含切线的平面）是垂直的。

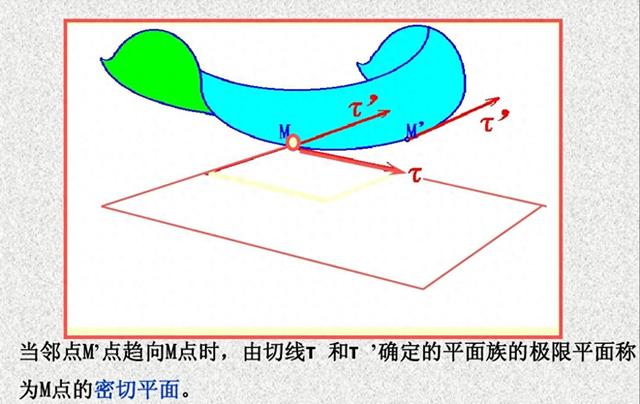
这里的R-r，在密切平面中就表示的是密切平面中的向量，如下图：

同样，在法平面和从切平面中，也表示在各自平面中的向量。

综上所述，密切平面、从切平面和法平面是描述空间曲线在某点附近几何性质的重要工具。它们分别反映了曲线在该点的弯曲情况、切线方向以及法向性质。