大家好,我是超自然现象探索官,感谢您的观看,希望能得到您的一个"关注"
数学在现实世界中的应用程度令人惊奇。不知何故,我们人类已经开发出了一套逻辑规则系统,可以很好地描述宇宙。关于我们发明了多少数学以及发现了多少数学,一直存在着争论。这场争论涉及的主要数学对象之一是黄金比例。

黄金比例具有一些独特的属性,因此它出现在各种各样的情况下。人们第一次注意到它是在公元前 300 年的欧几里得著名的《几何原本》中,从那时起它就一直很重要。尽管黄金比例长期以来在数学中很重要,但据说黄金比例也出现在建筑、音乐、物理和许多自然环境中。然而,最近的研究表明,其明显的普遍存在可能被夸大了。由于其有趣的视觉结构,它已成为流行数学中非常受欢迎的话题。
显然,黄金比例涉及更深层次的东西。但这个神秘数字中蕴藏着怎样的真相呢?它是基于实际观察还是只是一个流传已久的神话?在这篇文章中,我将描述黄金比例到底是什么。然后我们将看看它的一些用途,以及它绝对不适用的地方。这是一个有趣的话题,所以让我们开始吧。

黄金比例是两个数字之间一种非常特殊的关系。它可以用数学表达如下:

黄金比例 要创建黄金比例,您需要两个数字:a 和 b,使得 a 与 b 的比率等于 a + b 与 a 的比率。数学家选择希腊符号 φ 来表示这个数字。事实证明,我们可以通过操纵这两个分数来求解 φ 的方程,得到以下方程:

我们可以将这个关系转换成多项式,并使用二次方程得到以下答案:

有趣的是,黄金比例是一个无理数。这意味着它不能表示为整数之间的分数,并且它的小数形式将无限期地继续下去,没有任何模式。上面的分数不算数,因为分子有平方根。这就是黄金比例。如果您不懂数学,请不要担心。我认为下面的几何解释会更直观。

基本上,红色矩形的比例与红+蓝色矩形相同。我们只需要旋转较大的矩形并使其变小一点即可得到红色矩形。这一特性赋予了黄金比例美丽,并使其具有视觉吸引力。这就是您了解基础知识所需了解的全部内容。让我们看看这与另一个非常流行的数学对象有何关系。

与黄金比例最令人惊讶的联系之一是与斐波那契数列的联系。您以前可能听说过这组数字,但如果没有,请不要担心!斐波那契数列的定义非常简单且易于理解。每个数字都是通过将序列中的前两个数字相加而创建的。我在下面显示了前几个数字。

至少从公元前 200 年起,这个序列就已为人所知,当时它在古印度文献中已有描述。有趣的是,当我们浏览序列时,每个数字与其前一个数字的比率接近黄金比例。我们用数学方式表达如下:

其中 Fₙ 是上式中斐波那契数列中的第 n 个数。您可以在上图中看到这个比例。每当螺旋形成一个新数字时,就会创建一个矩形。每个新的矩形都越来越接近我上面描述的黄金比例矩形。
如果您对限值指定感到困惑,请查看下表。每个划分都越来越接近黄金比例。
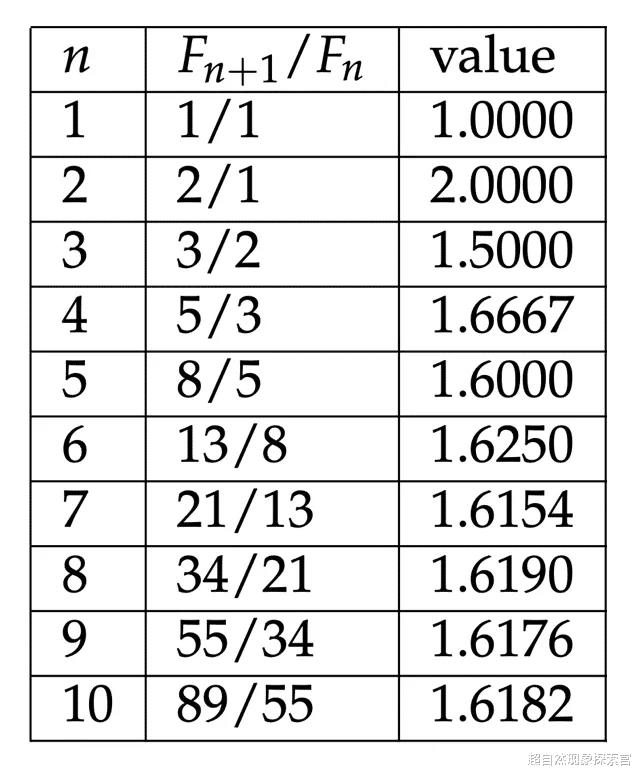
到目前为止,我们已经讨论了隐藏在黄金比例中的两个主要数学思想。让我们看看如何使用这个概念来创建美观的设计。

一些杰出的艺术作品都使用黄金比例来传达美感。达芬奇因对黄金比例的痴迷而闻名,他花费了大量的精力试图找到视觉上传达黄金比例的最佳方式。大多数艺术家以两种方式使用黄金比例。他们要么使用由一系列不断增加的矩形创建的黄金螺旋,如上图的画作“神奈川巨浪”所示。艺术家还使用黄金矩形,它只是遵循这一比例的一个矩形。

(来源)例如,萨尔瓦多·达利的《最后的晚餐》通过将桌子放置在创建它所需的确切位置来使用黄金矩形。我们知道,这个安排是他故意的。这幅画中还有许多由学生们布置创作的其他黄金矩形。
现在重要的是不要夸大黄金比例的使用频率。许多关于黄金比例的说法根本没有得到证实,而是通过在图像上叠加螺旋来证明其合理性。螺旋必须具有非常特定的形状才能被视为黄金。
尽管达芬奇痴迷于黄金比例,但我们从他的著作中知道,并不是每部作品都旨在代表黄金比例。流行的数学著作经常提到他的《维特鲁威人》和《蒙娜丽莎》作为黄金比例的其他例子。同样,这些说法仅通过图像上螺旋的叠加来证明是合理的,并且根本经不起数学审查。
其他研究试图衡量不同矩形的美观程度,看看黄金矩形是否胜出。结果有些好坏参半,但大多数人并没有发现对黄金矩形有强烈的偏好。我在文章末尾提供了这些研究的链接。
虽然黄金矩形可能不像热门文章让您相信的那样重要,但它仍然很特别。无可否认,它在美学上令人愉悦,并且与斐波那契数列有着深厚的联系。我们只需要小心不要夸大其重要性。让我们看看这种联系是如何导致自然界中出现这种比例的。

正如我之前提到的,螺旋形状并不一定意味着黄金比例起作用。然而,黄金比例和斐波那契数之间的数学联系意味着这种关系在自然界中明显存在。
斐波那契数列实际上存在于自然界中。通常,当植物试图最大限度地获得阳光或有效地生产种子时,斐波那契数列很有用。

蓝色和浅蓝色的两个旋臂方向相反。每种类型有 21 和 13 个,明显是斐波那契数。葵花籽也遵循类似的螺旋图案,一个方向有 34 个臂,另一个方向有 55 个臂,这也是斐波那契数列。
出现这种模式是因为植物以向外的螺旋模式生长。由于斐波那契数列的基本特性,它可以以这种方式生长并产生最大数量的种子。既然黄金比例是相关的,这就是这种关系的自然表现。

松果表现出相同的结构,并创建与斐波那契数相对应的螺旋投影集。
一般来说,黄金比例和斐波那契数确实出现在自然界中。它们的数学特性使它们对某些物种有用,虽然我没有在这里讨论它,但有些晶体遵循这种模式。然而,它们的重要性可能被夸大了。可能与美有一些联系,但联系并不紧密。这可能是流行文化传播的数学神话,就像《达芬奇密码》中那样。
