仿射变换的优点主要包括以下几点:
保持图形的“平直性”和“平行性”:仿射变换在保持图形的直线和平行线性质不变的前提下,可以进行各种线性变换和位移,这使得它在图形处理中非常有用。实用性广泛:仿射变换在图像处理中有广泛的应用,如图像配准、图像纠正和纹理纠正,以及创建全景图像等1。此外,它还可以用于计算机视觉中的特征提取和模式识别。数学表达简洁:仿射变换可以通过一个3x3的变形矩阵来表示,这使得其在数学处理上非常方便和高效。参数少且易于计算:仿射变换只需要6个参数(在齐次坐标下),这使得计算相对简单,并且可以通过少量的控制点对来估计变换矩阵。下面是仿射变换的两个定理。
定理一:在透视仿射下,任何一对对应点到对应轴的距离之比是一个常数。


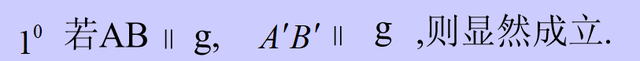

由相似三角形得:
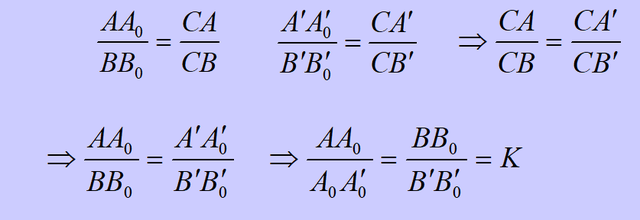

定理二:任意两个三角形面积之比是仿射不变量。
证明:
分两种情形。
1、特殊情形:有两对对应点在对应轴g上并且重合.如图


2、一般情形:如图

由1、的证明可得:


推论1:在仿射变换下,任何一对对应多边形面积之比是仿射不变量
推论2:在仿射变换下,任何两条封闭凸曲线所围成的面积之比是仿射不变量
