仿射不变性与不变量:经过一切透视仿射不变的性质和数量。
两直线间的平行性是仿射不变性。
要证明两直线间的平行性是仿射不变性,可以按照以下步骤进行:
假设与设定:
设a和b是平面α内的两条平行线。α'和b'是它们在平面α内的仿射映像。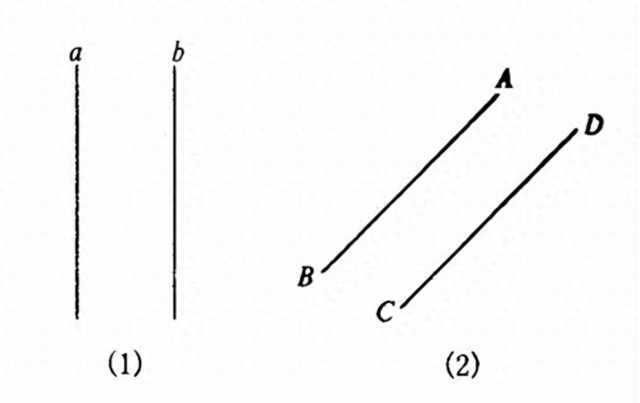
反证法证明:
假设a'与b'不平行,而是相交于一点P'。设P是P'的原像点,即P是a和b上的点,通过仿射变换得到P'。利用仿射变换的性质:
由于仿射变换保留接合性,点P应该既在a上又在b上。这意味着a和b是相交的,而不是平行的,这与我们的初始设定矛盾。得出结论:
由于我们找到了矛盾,所以假设不成立,即a'与b'必须是平行的。因此,我们证明了两直线间的平行性是仿射不变性。
请注意,仿射变换包括平移、旋转、缩放以及剪切等操作,但它保持了图形的直线性和平行性不变。这一性质在图形处理、计算机视觉等领域有着广泛的应用。
仿射不变性还包括:
仿射图形:经过任何仿射对应不改变的图形。
仿射性:经过任何仿射对应不改变的性质。
仿射量:经过任何仿射对应不改变的数量。

