




因为

而我们知道,闭集的补集是开集。所以我们又有



有理数在数学上不是连通的。
在数学中,连通性是指一个集合不能被划分为两个不相交的开集。有理数集合(Q)可以被无理数分隔成两个不相交的部分,因此有理数集合不是连通的。
具体来说,对于任意一个无理数e,有理数集合Q可以被分为两个开区间(-∞, e)和(e, ∞),这两个区间是不相交的,因此有理数集合Q不是连通的。此外,有理数在实数轴上的分布是稠密的,但这种稠密性并不意味着它们是连通的。有理数之间的空隙非常大,每个有理数之间的空隙都充满了无理数,这使得有理数集合在实数轴上不能形成一个连续的整体。
实数集R是连通的:

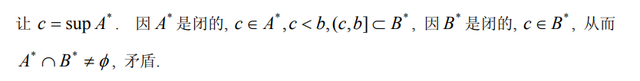
这里的关键在于,当c是A的上确界时,(c,b]肯定是属于B*的,这是因为

同时又因为B是闭集,从而得到c属于B*这个矛盾的结论。


习惯一个人
陀螺仪在当今社会应用很广,陀螺仪其中一个基本特性:定轴性,当陀螺转子以高速旋转时,在没有任何外力矩作用在陀螺仪上时,陀螺仪的自转轴在惯性空间中的指向保持稳定不变,即指向一个固定的方向;同时反抗任何改变转子轴向的力量。这种物理现象称为陀螺仪的定轴性或稳定性。其实以上的基本特性描述是不严谨的,以上的基本特性描述是只有在转子轴向在大于0度小于90度范围内才可以成立的,在大于等于90度小于180度范围内是不成立的,在夹角等于90度时反抗任何改变转子轴向的力量大小和方向无法确定(有点像薛定谔的猫),当夹角稍微大于90度时反抗任何改变转子轴向的力量大小和方向确定,不在是保持陀螺仪的自转轴在惯性空间中的指向保持稳定不变,而是指向一个固定的相反方向,明显可以重复观察到,网上有卖金属倒立自动翻转陀螺可供参考,是最典型的实践证据。自动翻转陀螺在翻转的同时重心增高,势能变大,传统物理学理论无解。 陀螺仪的定轴性,在反抗任何改变转子轴向过程中如果不存在重力以外的外力,定轴性表现是和轴向角动量守恒是冲突的,和牛顿第二定律是冲突的。研究结果可以理论个实验重新定义 时间 和 空间。