在美剧《老友记》第5季第16集中，男主角罗斯买了一张新沙发，于是他找来了两个朋友，让他们帮忙把沙发抬进公寓中。 在抬着沙发经过楼梯拐角处时，罗斯对着他的两个朋友大喊：“Pivot！Pivot！”（Pivot的意思是绕某个中心轴转动），然而，由于沙发比较大，他们如论如何也无法使沙发顺利通过拐角。 罗斯搬沙发的故事成为了剧迷们津津乐道的一个笑料，但其实，这不能怪罗斯，因为搬沙发通过拐角可不像看起来那么简单，这涉及数学领域的一个难题——移动沙发问题。 移动沙发问题来源于现实生活中推沙发经过走廊拐角的情景，但做了一些理想化的处理，比如走廊拐角和沙发都被考虑成了二维平面。移动沙发问题是这样描述的：求能通过单位宽度（即宽度为1）的L形平面通道的刚性二维形状的最大面积。 用直白的语言描述下，就是有一条宽度为1的直角走廊，如果一个沙发（沙发是刚体，不能被挤压变形）能通过，那么这个沙发的最大面积是多少？ 移动沙发问题最早在1966年，由加拿大数学家利奥·莫泽提出。 1968年，英国数学家约翰·哈默斯利提出了一种简单的解法。他设计了一个老式电话听筒形状的“沙发”，由两个1/4圆和一个被挖去半圆的的矩形组成。哈默斯利得出结论：“沙发”的最大面积为 2.2074。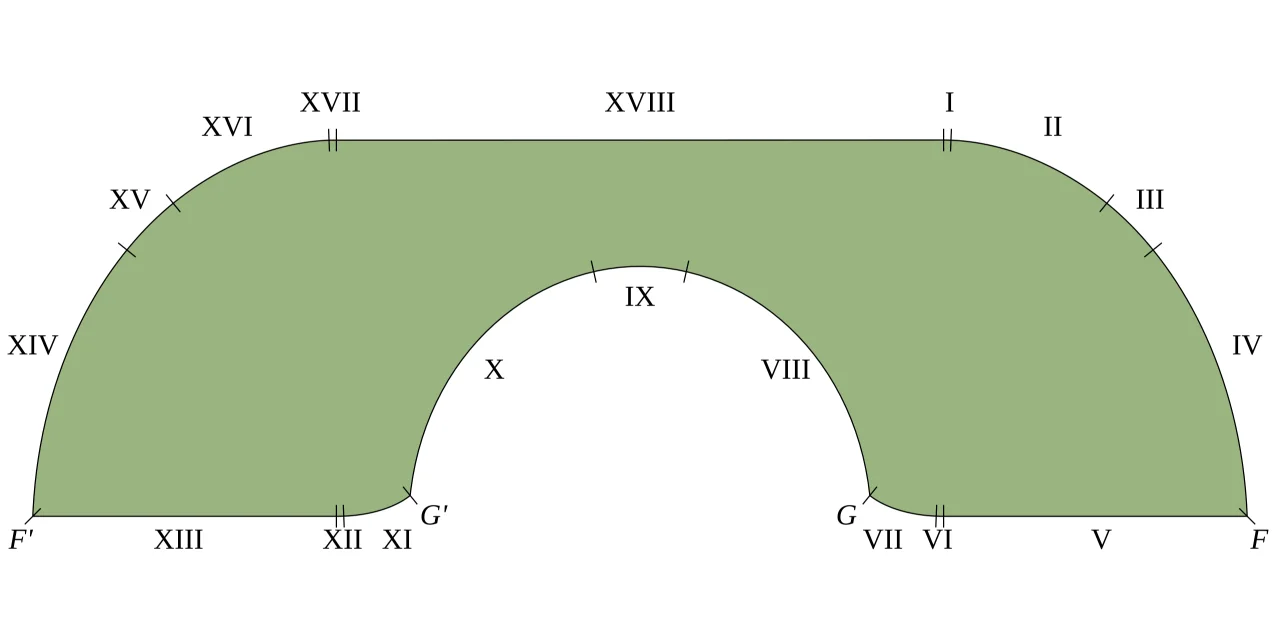 1992年，美国数学家约瑟夫·杰弗改进了哈默斯利的“沙发”，他提出了一种由18条光滑曲线段围成的“新沙发”，面积为2.2195，比哈默斯利的略大。但当时杰弗无法证明他的“沙发”是面积最大的。 2024年12月2日，韩国延世大学的数学研究员白真允宣称解决了移动沙发问题。他在论文预印本网站发表了一篇题为“Optimality of Gerver’s Sofa”的论文，声称美国数学家约瑟夫·杰弗是对的，即移动沙发问题的最优解是2.2195。 白真允的论文中有非常复杂的数学证明，总共有119页。但这篇论文尚未经过其他数学家的评审，结果是否正确，有待进一步验证。 如果白真允的论文结果是正确的，那么，《老友记》中的罗斯就知道该买什么样的沙发，才能顺利搬进公寓了。不过，在现实生活中，沙发制造厂可能不会生产这种造型奇怪、实用性也不强的沙发。 移动沙发问题不仅仅是一个纯粹的数学难题，研究这个问题对我们的实际生活也有重要意义。比如，通过解决这个问题，科学家可以知道如何让物体更有效地通过有限的空间，这可能在智能驾驶、导航等领域派上用场。