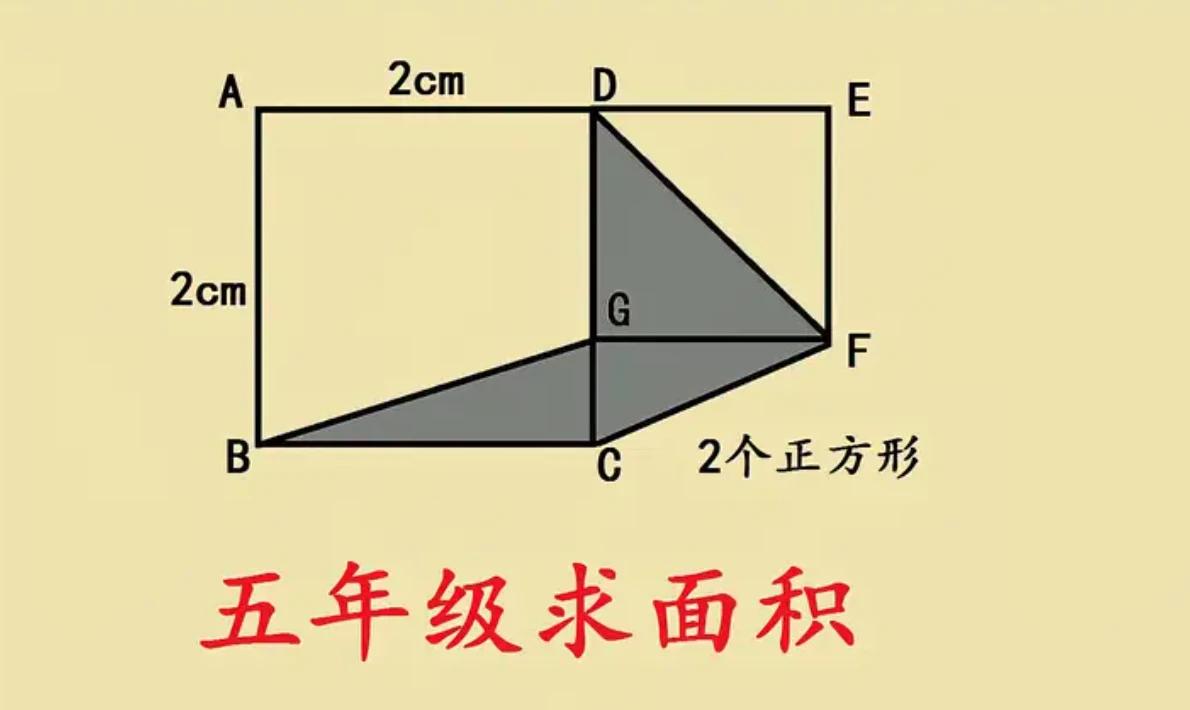
五年级期末考试附加题，难哭众多学霸，看似简单的题目，很多学生硬是没有找到解题的突破口。 如图所示，两个正方形并排摆放，求阴影部分面积？ 题目只告诉了大正方形的边长是2厘米，那么阴影部分势必和大正方形面积有关联，我们不妨通过辅助线利用面积转换解题。#五年级几何题# #分享小学数学题#
五年级期末考试附加题，难哭众多学霸，看似简单的题目，很多学生硬是没有找到解题的突
大力小学数学吖
2024-10-23 11:47:08
1
阅读：423
用户10xxx48
2c㎡
我的UC 回复 11-26 15:43
简单直接[点赞]
千金散尽还复来
连接AG，三角形ADG与三角形DFC等底(都为大正形的一条边)，而且等高(都要小正方形的边长)三角形ADG的面积与三角形BCG的面积之和为大正方形面积的一半。也就是说三角形DFC与三角形BCG面积之和(即阴影面积)是大正方形面积的一半
我的UC 回复 我结婚了 11-26 15:48
面积相等，用ADG替换DCF。
我结婚了 回复 11-21 22:07
后半部分没看懂呢，之和是一半？
山哥
做FG延长线相交于BD于H点，BHG面积和CGF相等DGH和DGF面积相等，得出阴影面积是大正方形一半
千金散尽还复来
连接AG，三角形ADG与三角形DFC等底(都为大正形的一条边)，而且等高(都要小正方形的边长)，三角形ADG的面积加三角形BCG的面积等于大正方形面积的一半。也就是说三角形DFC的面积加三角形BCG的面积(即阴影面积)等于大正方形面积的一半
仙家奇缘6
按图连接辅助线，得出△BCG=△BCH 则阴影部分面积可算！！
我的UC 回复 11-26 15:32
巧妙[点赞]
用户10xxx32
把大正方外面的二个阴影部分移进大正方形内，可以求出s阴=2X2÷2=2平方厘米
子鱼
延长FG与AB相交与E，容易求的BCG是小矩形BCGE面积一半，DFC是ADGE面积的一半，阴影面积2
珠乡俗人
连接cd作辅助线，三角形bdg和cdf的面积相等，阴影部分面积就是大正方形面积的一半，2平方厘米
傻得有水平
先等面积变换，凑成一个三角形△ACF，因为AC∥DF，所以S△ACF=S△ACD=2×2/2=2
流水哥哥
这题的难点主要在于视觉效果！让学生思维很容易往立体感上面去想！
我结婚了
评论区的都是考上大学了吗？
我的UC
面积2
用户47xxx27
右边阴影△CDF的底是大正方形的边长，高是小正方形的边长，也就是△ADG的面积。