C^k微分结构是用一个C^k-图册定义的，这个图册是在流形M的一些子集（这些子集的并集是整个M）与n维向量空间的一些开子集之间的双射集合（称为坐标卡）。这些坐标卡需要满足C^k-相容的条件，即当两个坐标卡的定义域有交集时，它们之间的转移映射（即一个坐标卡映射下的像到另一个坐标卡映射下的像的映射）需要有k阶连续导数。

也就是说，

坐标卡相容是指在微分几何中，两个坐标卡在重叠区域内的坐标变换是连续的，即它们在重叠部分可以平滑地过渡，不会产生跳跃或断裂。这种相容性确保了在流形上的坐标变换是局部光滑的，从而使得微分几何的分析和计算变得可行。

这里转载网友的一个例子进一步说明：

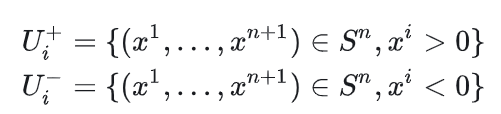
定义映射：

上面的映射相当于降维，而逆映射相当于升维。

先验证坐标卡的相容性：

可以得到：

同样：

以上的复合运算的结果还是相当于n维球面被降维。

这其实还是因为n维球面方程

具有n阶连续导数。

因此得到

微分结构，球面是一个光滑流形。

C^k微分结构本质上是一个满足一定条件的坐标卡集，涉及到多个映射和它们之间的关系（即相容性），而不仅仅是一个单一的映射关系。这种结构为在流形上进行微分运算提供了基础。