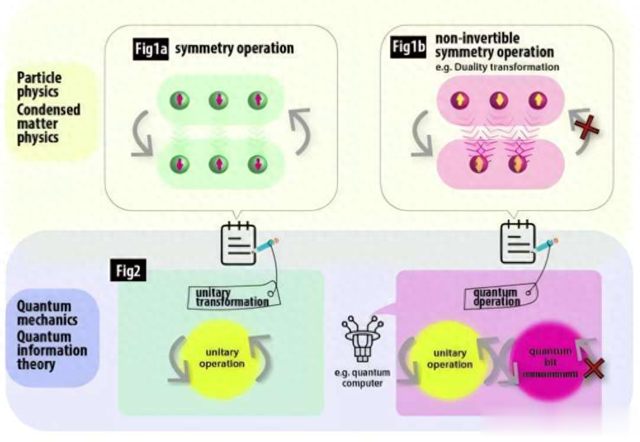
这项研究的总结表明，任何不可逆对称性的运算都是量子运算。图片来源：Kavli IPMU

理论物理学家在证明理论物理学中的任何非可逆对称操作都是量子操作后，在理论物理学中迅速发展的量子信息论和粒子和凝聚态理论中的不可逆对称性这两个领域之间建立了密切的联系。该研究于 11 月 6 日作为编辑建议发表在 Physical Review Letters 上。

在物理学中，对称性为理论的性质提供了重要线索。例如，如果磁场中的 N 极同时被 S 极取代，S 极同时被 N 极取代，则物体上的力和磁场中存储的能量保持不变，即使磁场的方向现在已经反转。这是因为描述磁场的方程式在交换 N 极和 S 极的操作方面是对称的。

在过去的几年里，对称性的概念在粒子物理学和凝聚态物理学的理论研究中得到了各个方向的推广，成为一个活跃的研究领域。一种这样的推广是不可逆对称性。传统对称性的操作总是可逆的。存在撤消操作。另一方面，不可逆对称性允许在这种对称操作中实现一定的不可逆性。

近年来，另一个越来越受到物理学家关注的领域是量子信息论。它是构成量子计算机基础的理论。

量子计算中的一个基本概念是执行各种运算量子比特，也称为量子比特。其中，任何可以撤消的操作都是由称为幺正变换的数学运算来表示的。然而，没有反向操作的非可逆操作也很重要，例如量子比特的测量。这些操作是使用幺正变换的广义概念（称为量子运算）执行的。

几年前，数学家 Marcel Bischoff 和他的合作者提出了一个想法，即不可逆对称性的运算是一种量子运算。然而，他们的想法是在仅适用于具有特定属性的物理系统的框架中描述的，并且大多数物理学界都不熟悉。

现在，两位研究人员，东京大学理学院研究生 Masaki Okada 和东京大学 Kavli 宇宙物理与数学研究所 （Kavli IPMU， WPI） 教授 Yuji Tachikawa 已经证明，这个想法可以在粒子物理学和凝聚态物理学中广泛使用的框架中得到很好的证明。

到目前为止，还没有人知道什么是不可逆对称操作的一般性质。冈田和立川的工作提供了一个答案，即任何不可逆对称性的运算都是量子运算。

更多信息：Masaki Okada 等人，非可逆对称性通过量子运算局部作用，物理评论快报（2024 年）。DOI： 10.1103/PhysRevLett.133.191602

期刊信息： Physical Review Letters