这里参考B站一位老师的讲解,给出黎曼曲率的一种解释。
先看协变导数的定义。由于
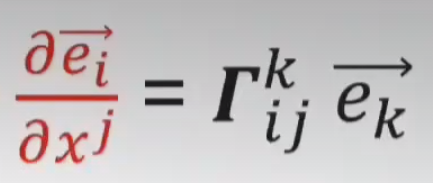
通过

得到


上图中,假设一个向量从A点出发,经过B、C、D后又回到A点,此时原向量发生了变化,变化量是dV。假设这个变化存在如下性质:


这里的λ表示出发向量的编号,ρ表示到达向量的编号。比如

表示出发向量是V0(A点向量),到达向量是V1(B点向量)。

如果是平直空间:

如果是曲面空间:

则要用到协变导数:

这里的▽u,▽v分别代表向量在水平方向和垂直方向发生的变化。

再与下式对比:

并代入协变导数

得到黎曼曲率:

所以黎曼曲率反映了向量在非平直空间移动后发生的改变程度。


王大勇
发光源在移动的时候,在运动前进方向上光的频率是会发生紫外频移的,在运动前进反方向上光的频率是会发生红外频移的,可以测速,即多普勒效应。现实中光速不是绝对的,请注意太阳系是运动的,银河系是运动的,在光速频移上就没体现出来,集体潜意识影响是巨大的。科研需要冲破集体潜意识。