拓扑学是研究图形（或集合）在连续变形下的不变的整体性质的一门几何学。它只考虑物体间的位置关系而不考虑它们的形状和大小。

“拓扑”是我们常常会听见一个数学名词，乍听起来，它好像是一个很“玄”的东西，但实际上它并不神秘，“拓扑”已经成为一种再基本不过的数学结构和数学语言，没有这样的基本结构，就不可能有今天的数学。

从定义上来说，拓扑是赋予在集合上的数学结构，在满足规定的三条公理后，这个集合连同这个结构就成为一个拓扑空间，这个结构就被称为“拓扑”。也就是说，“拓扑”是人为规定出来的一种结构，它的基本组成元素是所谓的“开集”。

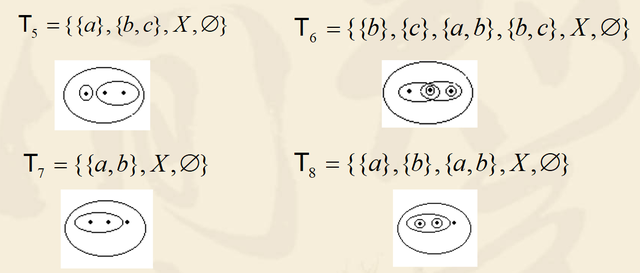
当然，通过对以上拓扑中a,b,c的不同排列，我们在X上还可建立其它拓扑结构.但是,并不是X的每个子集族都是X的拓扑。

例如，下面的两个X的子集族就不是X的拓扑：

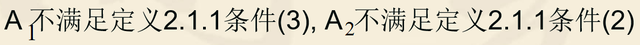
A1：{a}和{b}的并集{a,b}不属于 A1。

A2:{a,b}和{b,c}的交集{b}不属于A2。