近日，“8个瑞士卷怎么分？”这一词条冲上热搜，引起广泛的关注和讨论。

瑞士卷也是蛋糕的一种，所以瑞士卷的分配问题也算是分蛋糕问题（欸嘿）。

实际上，分蛋糕（cake cutting）这一问题并非只在现在引发讨论，从上个世纪以来，数学家、经济学家、计算机科学家、社会科学家开始研究公平分配资源的方法，切蛋糕的思考是一个庞大的数学分支领域的一部分，它催生了大量算法，指导人们应用在生活的方方面面。

小编和朋友们一起分的蛋糕，切得可谓惨不忍睹

那么接下来，我们先从最简单的模型开始——两个人如何分蛋糕？

两人分蛋糕

假如两个人都要吃一块蛋糕，且两个人都是“理性人”（追求自身利益最大化的理性主体人），要如何分配，才能让两个人都满意？

简单思考就可以发现，只需要使用“我来分，你来选”的方法就可以解决。

A：磨刀霍霍向蛋糕

首先，由其中一人A把蛋糕分成两块，然后，另一个人B选出自己更想要的那一块，剩下的留给第一个人A。由于分蛋糕的人A并不知道B会选择哪一块，为了保证自己的利益，他会把蛋糕分成均等的两块。这样，不管对方选择了哪一块，他都能保证自己总可以得到蛋糕总价值的一半。

三人分蛋糕

人数来到了三个人，蛋糕的分配就变得复杂了起来。在这里，“如何让三个人都满意”在数学上有多种涵义，常用的两种是：

均衡分割（proportional）：三个人都认为自己得到了整个蛋糕至少1/3的价值。

无嫉妒分割（envy-free）：三个人都认为别人的蛋糕没我手里的多。

无嫉妒一定均衡，但是无嫉妒不一定均衡。在这两种解释下，有不同的分配策略。

（当然，这种分配策略不可能是刘星分饼法）

既然提到了刘星分饼，不如我们让家有儿女的三位孩子们分一块蛋糕吧！刚好三个人！

我们仨分蛋糕？真的假的

均衡分割可以采用“最后削减人算法”。

1.第一个人A从蛋糕中切出他所认为的 1/n ，然后把这一小块传给第二个人B。

2.第二个人B可以选择直接把这块蛋糕递交给第三个人C，也可以选择从中切除一小块（如果在他看来这块蛋糕比 1/n 大了），再交给第三个人C。以此类推，每个人拿到蛋糕后都有一次“修剪”的机会，然后移交给下一个人。

3.规定：最后一个对蛋糕大小进行改动的人将获得这块蛋糕，余下的n-1个人则从头开始重复刚才的流程，分割剩下的蛋糕。每次走完一个流程，都会有一个人拿到了令他满意的蛋糕，下一次重复该流程的人数就会减少一人。不断这样做下去，直到每个人都分到蛋糕为止。

第一轮流程结束后，拿到蛋糕的人可以保证手中的蛋糕是整个蛋糕价值的1/n 。而对于每个没有拿到蛋糕的人来说，由于当他把蛋糕传下去之后，他后面的人只能减蛋糕不能加蛋糕，因此在他看来被拿走的那部分蛋糕一定不到 1/n ，剩余的蛋糕对他来说仍然是够分的。

在此游戏规则下，大家会自觉地把手中的蛋糕修剪成自认为的 1/n ，耍赖不会带来任何好处。分蛋糕的人绝不敢把蛋糕切得更小，否则得到这块蛋糕的人就有可能是他；而如果他把一块大于 1/n 的蛋糕拱手交给了别人，在他眼里，剩下的蛋糕就不够分了，他最终分到的很可能达不到 1/n 。

无嫉妒分割中，可以将“蛋糕”分为离散和连续两种情况。

离散程序

1960年John Selfridge和 John Conway 各自独立构造出了第一个满足免嫉妒条件的三人分割方案。这种分割方案被称为“Selfridge-Conway算法”。

1.A夏雪把蛋糕分成三等份①、②、③。

2.如果 B 刘星认为这三块蛋糕中较大的两块②、③是一样大的，那么按照C夏雨、B刘星、A夏雪的顺序依次选取蛋糕，分配结束。

3.如果B刘星认为较大的两块蛋糕②、③不一样大，那他就把最大的那块蛋糕③的其中一小部分切下来，让剩余的部分③’和第二大的蛋糕一样大。将切下来的小部分标为④，待会再来处理它。

4. 按照C夏雨、B刘星、A夏雪的顺序依次选蛋糕，但有一个限制：如果C夏雨没有选那块被修剪过的蛋糕③’，B刘星就必须选它。

到此为止，三人都拿了一块蛋糕。因为A夏雪是切蛋糕的人，在她眼里三块是一样大的，所以拿到哪一块都一样，因此她不会嫉妒别人；B刘星将两个较大蛋糕修剪成一样大，他选取了较大块中的一个，他也不会嫉妒别人；C夏雨是第一个选蛋糕的人，显然他也不会嫉妒别人。目前来看，三个人是满足无嫉妒分割的。

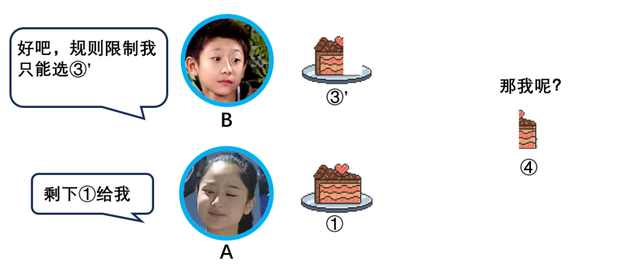
接下来，我们再处理没分割完的一小块④：

5.在刚刚的选择中，B刘星选择了那块被修剪过的蛋糕③’，而C夏雨选择了没有被修剪过的②。让C夏雨把最后的那一小块④分成三等份，按照B刘星、A夏雪、C夏雨的顺序依次挑选蛋糕。

分完最后的小块后，每个人又得到了一小块蛋糕。在这一轮挑选中，B刘星是第一个挑选的人，显然他不会嫉妒别人；而C夏雨是三等分④的人，在他眼里等分三块一样大，他也不会嫉妒别人；由于A夏雪比C夏雨先选，A夏雪不会嫉妒C夏雨，且A夏雪也不会嫉妒B刘星，因为即使B刘星拥有了第二轮中的全部蛋糕，B刘星手里的蛋糕加起来也只是第一轮开始时A夏雪三等分出来的其中一块蛋糕，这是不可能超过A夏雪的。因此，三个人依然不会嫉妒彼此。

走刀（连续）程序

在上个世纪80年代，由Stromquist提出了无嫉妒分割的另一种解：走刀程序（Moving-knife procedure）。在这个程序里，我们将用矩形的蛋糕进行演示。

1.让我们找一个裁判（就是你了，夏东海爸爸！）。爸爸拿着刀，从蛋糕的最左边缓缓向右移动。

2.A夏雪、B刘星、C夏雨三个人也拿着刀，站在爸爸的右边，随着爸爸从左向右移动，三人分别站在他们认为能够二等分爸爸右侧蛋糕的位置（按各自的标准）。

3.在移动过程中，当有人（假设是B刘星）是认为爸爸已经移动到了整个蛋糕1/3的位置时，他大喊一声：“停！”，此时爸爸将手中的刀切下去，而三个人中位于中间的人（假设是B刘星）也切下刀。

4.此时蛋糕通过两刀被分成三块，根据以下规则分配蛋糕：喊停的人B刘星拿走最左侧的一块，离裁判近的人（假设是C夏雨）拿走中间的一块，离裁判远的人（假设是A夏雪）拿走最右侧的一块。

在这种分法中，三个人依然不会嫉妒彼此：

A夏雪、C夏雨：我没有喊停，因为我心中自己得到的部分比左侧蛋糕大，且我现在得到的蛋糕比我刀能切下的部分还大，我肯定不会嫉妒你们。

B刘星：我喊停了，因为我认为蛋糕已经达到我不叫停时能获得的部分，且大于等于剩下的部分，所以我觉得我拿的是最多的。

当然当然，走刀的操作方法的可操作性很低——又有谁能肉眼预判自己是否正好处于爸爸右侧的中间呢？所以它更多是一种抽象的数学模型。

博弈论中的“分蛋糕博弈”

在经典博弈论中，也有不同前提条件的分蛋糕问题。简单介绍两种如下：

两个参与人分割一块蛋糕，参与人1先出分配方案，参与人2选择接受或拒绝；如果拒绝参与人2提出分配方案，参与人1选择是否接受；依次类推，直到某个参与人的方案被接受。且此时会出现成本：蛋糕在融化，决策时间越长，集体的收益将减少。

这是一个完全信息动态博弈（完全信息：参与人各方对其他参与人的特征、策略空间和收益函数等信息都有准确的了解；动态：博弈中参与人的行动存在先后顺序，且后来采取行动者能够通过观察知道先行动者的行动），可以通过博弈论的方式，得到其纳什均衡（每个参与人的策略选择，都是对于对手策略选择的最佳策略选择）。

两个人分一块蛋糕，两人各自独立地提出自己要求的份额x，x，如果x+x≤1，每人能得到自己要求的份额；否则，两人都啥也得不到。这个博弈有无数个纳什均衡，只要满足x+x=1即可，但让所有的局中人都预测到同一个纳什均衡是非常困难的。

当然当然，分蛋糕问题从来都不是一个绝对的数学问题，数学模型的处理忽略了太多实际的社会学因素：如果一块蛋糕上有个草莓，这块蛋糕对我的价值是否更多？更重要的是，生活中大家并不完全遵循着自私的“理性人”来决策：是否会因为喜欢对方，想让对方多吃一些？“觉得公平”的结果常常并不是精确的三等分，关键在于协商的机制合理，参与人互相认可。

都这么麻烦了，不如直接日~的一声打成糊糊吧！

“说吧，这次又要用我打什么？”

编辑：花卷