此前发布了一道六年级数学题:正方形内三角形的三边均未知,咋求其面积?娃费了九牛二虎之力、耗时近半个小时,好歹算做出来了!此题难度不算很大、但伤害值高,正确率极低、不到10%!
六年级数学:如图一,

图一
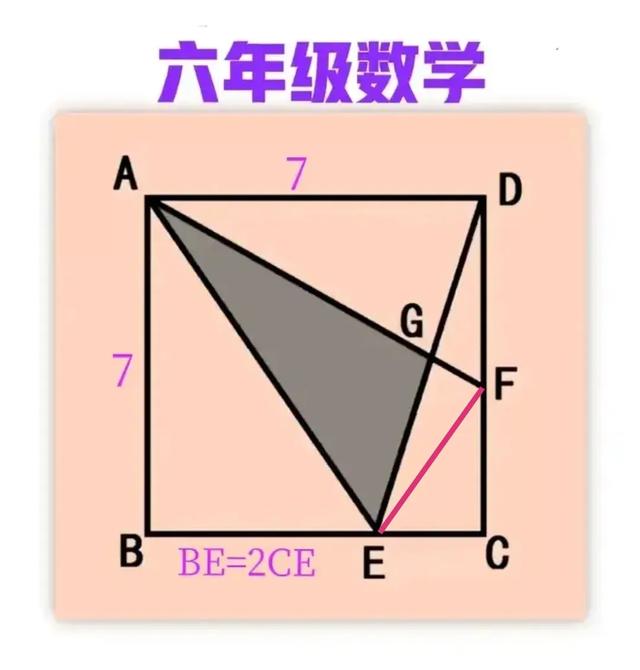
正方形ABCD的边长为7,点F为CD的中点,点E在BC上,BE=2CE,连接AF和DE相交于点G,连接AE。求灰色阴影三角形AEG的面积。
难点:①求S△ADG/S△AEG!②不能使用平行线段比、相似比等超纲知识!
误区:先求DG/EG,再求S△ADG/S△AEG!
事实上,仅用小学知识即比例计算,由S△ADF/S△AEF无法直接求出DG/EG,还需用到中学阶段知识比例性质、或相似比、或平行线段比!
一、超纲解析之一:先求DG/EG,需用到超纲知识①:若b/a=d/c,则(b+d)/(a+c)=b/a=d/c!
①连接EF,如图二
图二
②由BE=2CE及F为CD的中点可知,S△ABE=1/3S正ABCD,S△ADF=1/4S正ABCD,S△CEF=1/12S正ABCD。故S△AEF=1/3S正ABCD。
③S△ADF/S△AEF=3/4。
④将DG和DE分别视为△ADG和△AEG的底边,则两三角形等高,故其面积比等于底边之比也即有S△ADG/S△AEG=DG/EG。同理可得S△DFG/S△EFG=DG/EG。注意到S△ADF=S△ADG+S△DFG,S△AEF=S△AEG+S△EFG,由③和超纲知识②即得,
DG/EG=S△ADF/S△AEF=3/4。
⑤S△ADE=1/2S正ABCD,故S△AEG=4/7S△ADE=2/7S正ABCD=2/7×49=14。
二、超纲解析之二:先求DG/EG,需用到超纲知识:平行线段比或相似比!
①延长AG与BC、相交于点H。如图三

图三
①由F为CD的中点,可知CH=AD,AF=FH。
②EH=4AD/3也即AD/EH=3/4,故由超纲知识相似比或平行线段比,可得DG/EG=AD/EG=3/4。余下步骤同于超纲解析一。
三、不超纲解析:不求DG/EG,直接求S△ADG/S△AEG!
①连接EF,同于超纲解析一中步骤①②③可得S△ADF/S△AEF=3/4。
②由同底三角形面积比等于高之比,求得△ADF与△AEF对应公共底边AF的高之比等于S△ADF/S△AEF。
③由同底三角形面积比等于高之比,求得S△ADG/S△AEG等于两三角形对应公共底边AG的高之比S△ADF/S△AEF,即S△ADG/S△AEG=S△ADF/S△AEF=3/4。余下步骤同于超纲解析一。
注1:由上述不超纲解析也可求出DG/EG!事实上,由等高三角形面积比等于底边之比,即得DG/EG=S△ADG/S△AEG=3/4。
注2:综合上述三种解析来看,先求DG/EG的话,大概率要使用超纲知识!
—————————————————
友友们有好的思路或方法,欢迎留言分享!
