射影几何的建立主要是为了解决实际问题，特别是在绘画和建筑中的应用。

射影几何的起源可以追溯到透视法和投影法的需要。在文艺复兴时期，画家和建筑师需要解决如何在二维画布上忠实地再现三维现实世界的问题。阿尔贝蒂在1435年写成的《论绘画》一书中详细阐述了这一问题，提出了通过插进一张直立的玻璃板来模拟光线投影的方法，从而在画布上获得一个真实的截景。这种需求推动了射影几何的发展，使其成为一门研究图形在投影和截影下的性质和不变量的学科。

射影几何的核心思想是研究图形的射影性质，即图形在射影变换后依然保持不变的性质。保持关联关系是射影变换的一个基本性质，这些概念和方法不仅在几何学中有重要地位，也在视觉艺术中扮演关键角色。

射影几何的建立和发展不仅解决了实际问题，还推动了数学和艺术的发展。它通过无穷远点及图形连续变动的思想引入了新的数学概念和方法，标志着高等数学的发展。

平行射影的概念很简单，就是从一条直线上不同的点按照同一个方向在另一条直线上找到对应的点，而这个方向与这两条直线都不能平行。

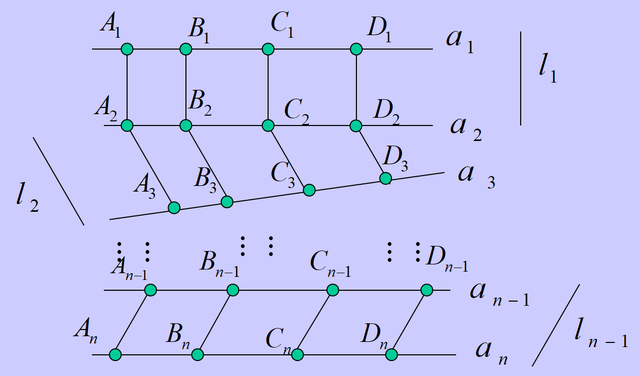
仿此，每一个对应点都可以这样表示。

1.仿射是有限回的平行射影组成的。

2.判断仿射是否是透视仿射的方法：对应点的联线是否平行。

3.书写的顺序与平行射影的顺序是相反的。

简单来说，仿射就是平行射影进行多次得到的结果。

再看两平面的平行射影与仿射对应：

两相交平面的交线为自对应点的集合即对应轴。

平面到平面的仿射是有限回平行射影的积组成的，是透视仿射链。

透视仿射具有如下性质：

1.透视仿射保留同素性.（几何元素保留同一种类而不改变）

即点对应点，直线对应为直线。

2.保留点与直线的结合性。