密度泛函理论 (density functional theory, DFT) 作为一种用于预测和解释材料性质的关键工具，在物理、化学、材料科学等领域都发挥着不可或缺的作用。然而，传统 DFT 通常需要耗费大量计算资源和时间，其应用范围受到显著限制。

作为一个新兴的跨学科领域，将深度学习与密度泛函理论结合，通过大量的计算模拟来预测和发现新材料，正逐渐克服传统 DFT 计算耗时且复杂的缺点，在计算材料数据库的构建方面具有巨大的应用潜力。神经网络算法加速构建更大规模的材料数据库，更大数据集又可以训练更强大的神经网络模型。然而，目前的深度学习 DFT 研究大多将 DFT 任务与神经网络分开处理，这大大限制了两者之间的协同发展。

为了将神经网络算法和 DFT 算法更有机地结合起来，清华大学徐勇、段文晖课题组提出了神经网络密度泛函理论 (neural-network DFT) 框架。该框架统一了神经网络中损失函数的最小化与密度泛函理论中的能量泛函优化，相比传统的有监督学习方法，具有更高的准确性和效率，为发展深度学习 DFT 方法开辟了一条新的途径。

该研究以「Neural-network density functional theory based on variational energy minimization」为题，发表在 Phys. Rev. Lett. 上。

研究亮点：

* 该研究提出了一种神经网络密度泛函理论的理论框架，将变分密度泛函理论与等价神经网络相结合

* 该研究基于 Julia 语言，结合 Zygote 自动微分框架，从头开发了一套名为 AI2DFT 的计算程序。在 AI2DFT 中，自动微分 (AD) 既可用于变分 DFT 计算，也可用于神经网络训练

论文地址：https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.133.076401

开源项目「awesome-ai4s」汇集了百余篇 AI4S 论文解读，并提供海量数据集与工具：

https://github.com/hyperai/awesome-ai4s

Kohn-Sham DFT 是材料模拟中应用最广泛的第一性原理计算 (ab initio calculation) 方法。该方法把复杂的电子相互作用问题简单化，将其映射为一个由有效单粒子 Kohn-Sham 哈密顿量描述的简化非相互作用电子问题，并且采用近似交换相关函数来考虑复杂的多体效应。虽然 Kohn-Sham 方程是从变分原理中形式化推导出来的，在理论物理学领域备受青睐，但由于迭代求解微分方程更为高效，该方法并不常用于 DFT 计算中。

然而，随着深度学习与 DFT 的进一步集成，这种开发范式已经得到了彻底改变。

深度学习 DFT 的研究主要依赖于数据驱动的监督学习技术。如下图 a 所示，一般情况下，传统的数据驱动监督学习方法通过对不同材料结构进行 DFT SCF 计算以生成训练数据，然后通过设计并训练神经网络，从而预测类似于 DFT 结果的数据。在这个过程中，神经网络与 DFT 是分开的。

深度学习与 DFT 集成的两种不同方法

现如今，如上图 b 所示，基于神经网络 DFT 的物理信息无监督学习，通过将 DFT 中能量泛函的优化与神经网络中损失函数的最小化相结合，实现了神经网络算法和 DFT 算法的共享与协同。更重要的是，通过将 DFT 明确引入深度学习，神经网络模型可以比先前的数据训练方法更好地模拟真实物理环境。

该研究选择了能量泛函 E[H] 进行后续研究，并采用 DeepH-E3 来确保映射 {R} → H 在三维欧几里得群中的协变性。

* DeepH-E3，徐勇团队基于等价神经网络设计的第二代 DeepH 架构。该框架利用三维欧几里得群下协变的神经网络预测微观原子结构对应的密度泛函理论 (DFT) 哈密顿量，极大地加速了第一性原理电子结构计算。

具体而言，如下图所示，该研究将等变神经网络以材料结构信息的嵌入作为输入条件，进而输出哈密顿量矩阵，获得神经网络权重参数化的 Hθ，能量泛函 E[H] 也可以被视为神经网络的损失函数 E[Hθ]。

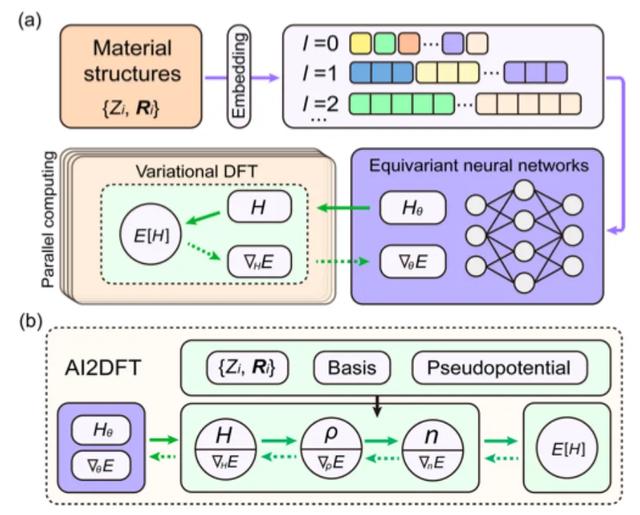
神经网络 DFT 的架构与实现路径

在神经网络 DFT 中，DFT 程序必须提供 ∇HE 以优化神经网络参数，这对于 DFT 编程而言是一个重大挑战。

尽管自动微分 (AD) 非常适合计算 ∇HE，但目前大多数 DFT 代码并不完全支持 AD 功能。因此，该研究使用 Julia 语言开发了一个自主可用的自动可微分 DFT 程序「AI2DFT」。值得注意的是，在 AI2DFT 中，自动微分 (AD) 既适用于 DFT 计算，也适用于神经网络训练。

在 DFT 中，AI2DFT 能够通过 H 推导出 ρ 和 n，从而计算出总能量，进而基于链式法则 (chain rule) 使用反向模式 (reverse-mode) 的 AD 依次计算 ∇nE、∇ρE 和 ∇HE 。在神经网络中，梯度信息 ∇θE 可用于神经网络优化。

在建立了神经网络 DFT 的理论框架，以及用可微编程的 AI2DFT 代码完成了数值实现后，该研究对 H2O 分子、石墨烯、单层 MoS2 和体心立方 Na 在内的一系列材料进行了全面测试。

具体而言，该研究首先检查了 AI2DFT 的 SCF 迭代是否能够很好地再现 SIESTA 代码的基准结果，然后应用变分 DFT 对相同的材料进行研究。如下图 a, b 所示，在数十个变分步骤后，总能量可以在 μeV 尺度以下收敛，能量梯度、哈密顿量、密度矩阵和电荷密度等其他物理量也表现出指数收敛，这验证了变分 DFT 的可靠性和鲁棒性。

AI2DFT 的验证

不仅如此，如上图 c, d 所示，与传统数据驱动的监督学习方法相比，AI2DFT 结合了变分 DFT 和 DeepH-E3 神经网络的性能。例如：

* 对于 H2O 分子，DFT 哈密顿量可以通过神经网络 DFT 优化，从而达到高精度，神经网络 DFT 的精度为 0.06 meV，数据训练的精度为 0.02 meV。

* 对于石墨烯，两种方法均达到了更高的精度，为 0.004 meV。因此，神经网络方法的可靠性得到了验证。

* 另外，在能量的预测精度 (prediction accuracy) 方面，神经网络 DFT 的性能显著优于数据训练。例如，对于 H2O 分子，神经网络 DFT 的能量预测精度达到 0.013 μeV，比数据训练的 0.83 μeV 高出 60 倍以上。

最后，该研究还将神经网络 DFT 应用于多种材料结构计算，并展现了无监督学习的能力。以 H2O 分子为例，如下图 a 所示，该研究首先通过基于 DeepH-E3 方法的数据驱动监督学习获得了预训练的神经网络模型，然后使用神经网络 DFT 对 300 个训练结构进行微调，实现了对哈密顿量及其他物理量的高精度预测。

使用神经网络 DFT 对多个 H2O 结构进行无监督学习

不仅如此，该研究还将训练后的神经网络模型用于预测训练过程中未见过的 435 个测试结构，结果也显示出良好的泛化能力，如上图 b, c 所示。与数据驱动的监督学习相比，神经网络 DFT 产生的哈密顿量虽然具有稍大的平均绝对误差，但在预测精度方面表现出优异的性能，这暗示了神经网络通过 neural-network DFT 过程学习到了更物理的模式。

由清华大学徐勇教授、段文晖教授领衔，汇集李洋、唐泽宸、陈泽洲等人的研究团队，在密度泛函理论 (DFT) 和第一性原理计算方面取得了一系列成果，他们的工作促进了深度学习技术在材料科学和物理研究领域的广泛应用。

自 2022 年起，徐勇和段文晖的研究团队就在第一性原理计算领域取得重大突破。他们开发了一种基于深度学习的理论框架和算法—— DeepH (Deep DFT Hamiltonian)。该方法充分利用了电子性质的局域性原理，只需要利用小体系数据集训练的模型便可以在大尺度材料体系给出准确预测，显著提升了非磁性材料电子结构的计算效率。

相关成果以「Deep-learning density functional theory Hamiltonian for efficient ab initio electronic-structure calculation」为题发表于 Nature Computational Science。论文链接：https://www.nature.com/articles/s43588-022-00265-6

2023 年，为进一步研究磁性材料的 DFT 哈密顿量对原子和磁结构的依赖关系，徐勇和段文晖的研究团队又提出了 xDeepH (extended DeepH) 方法。该方法通过一种深度等变神经网络框架来表示磁性材料的 DFT 哈密顿量，从而进行高效的电子结构计算。这一成果不仅为磁性结构的研究提供了一种高效且精确的计算工具，同时也为平衡 DFT 的精度与效率提出了一条可行路径。

相关成果以「Deep-learning electronic-structure calculation of magnetic superstructures 」为题发表于 Nature Computational Science。论文链接：https://www.nature.com/articles/s43588-023-00424-3

为了设计包含先验知识和对称性要求的神经网络模型，研究人员进一步提出了 DeepH-E3 方法。这种方法能够利用少量的 DFT 数据对小规模体系进行训练，然后快速预测大规模材料体系的电子结构。它不仅大幅提高了计算速度，达到了几个数量级的提升，而且在预测精度上也达到了亚毫电子伏的高标准。

相关成果以「General framework for E(3)-equivariant neural network representation of density functional theory Hamiltonian」为题发表于 Nature Communications。论文链接：https://www.nature.com/articles/s41467-023-38468-8

随着理论框架的持续优化，DeepH 已经实现了从非磁性到磁性材料的全面覆盖，并且在预测精度方面也得到了显著提高。在这样的背景下，徐勇和段文晖的研究团队进一步利用 DeepH 方法，构建出了一个 DeepH 通用材料模型。该模型能够应对包含多种元素和复杂原子结构的材料系统，并在预测材料性质方面展现出十分出色的准确性。

相关研究成果以「Universal materials model of deep-learning density functional theory Hamiltonian」为题发表于 Science Bulletin 上。论文链接：https://doi.org/10.1016/j.scib.2024.06.011

如今，徐勇、段文晖研究组又将神经网络算法和 DFT 算法进行有机结合，为发展深度学习 DFT 方法开辟了一条新的途径。毫无疑问，随着深度神经网络算法的不断进步和更大规模数据集的建立，AI 将变得更加智能，很可能在不久的将来，第一性原理计算、材料发现和设计都将由神经网络完成。这预示着 AI 将引领材料科学进入一个全新的数据驱动时代。