关于光速,有一个简单易记的描述:无论风向如何,光速始终如一,同样地,对于地球上的我们来说,光速也是不变的常量。

接下来,我们细致剖析这个议题,逐步进行解析。
设想一束光途经一阵风(不管是顺风还是逆风),对于风而言,光的速度恒为c,而对于我们这些地球上静止的观察者而言,光速同样为c。

再来看一束光相对于一辆高速行驶的车辆(无论车辆行驶方向与光束方向一致还是相反),其速度仍旧是c,而对于我们这些地球上静止的观察者而言,光速仍旧不变。
然而,当一束光与另一束光相遇(无论两者方向相同还是相反),事情就变得颇有意思了。
在处理这类光速问题时,许多人会不假思索地引用爱因斯坦的《特殊相对论》,并直接应用洛伦兹变换进行计算,看似轻而易举。然而,一个关键点却被忽略了。
实际上,洛伦兹变换或者说《特殊相对论》的推导基于两个基本公理——光速不变原理及相对性原理。

只有在满足相对性原理——即各参考系中的物理定律相同——的条件下,才能使用《特殊相对论》中的洛伦兹速度变换。风与人、车与人可被视为惯性参考系,但两束光之间则需另当别论。
以人作为观察者,一束光的光速为c,另一束亦然。按照这个逻辑,它们的相对速度似乎应为2c,也就是c加上c。
比如,想象一个光源同时向四面八方发射光,并在光源同一直线上等距设置两个敏感的光感设备。按照常理,设备测得的速度应为两个c,因为光速是恒定的,因此相对速度就是2c。
有人可能会质疑,2c岂不是超过了光速?其实不然,这仅仅是基于算术加法的简单推论,指的是两束光相对于静止观察者的速度之和,并不是指两束光之间的相对速度。
要计算两束光的相对速度,须以两束光各自作为参考系来进行分析。直接将光速代入洛伦兹速度变换公式中,得出两束光的相对速度实为c,而非2c,但其实c这个答案也不准确。

这是由于,在狭义相对论中,光不能作为参考系,因为光不遵循时间法则,光速是界定时空的关键。这就如同要求一个人既是运动员又是裁判员。我们还是先验证,再给出结论。

爱因斯坦提出,时间具有相对性。设想有人携带一个光钟搭乘飞船,地面上的观察者会发现,光钟不再垂直上下移动,而是呈现斜线轨迹。

基于光速不变原理,结合勾股定理,我们可以得出地球上的时间与飞船内的时间关系。
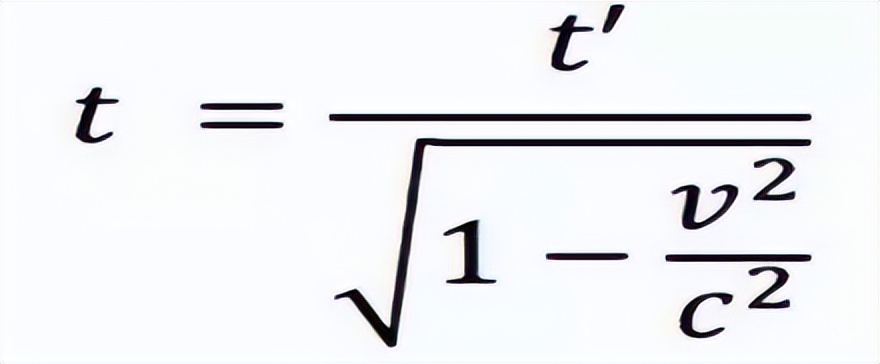
即时间膨胀公式如图所示,随着飞船速度逼近光速,飞船内的时间流逝与地球上的时间流逝比值也随之增大,若飞船速度等同于光速,飞船内的时间将趋于静止。

爱因斯坦提出的高速运动中时间流逝减慢的现象,根源即在于此。

综上所述,对于光而言,时间仿佛凝固,对于我们来说,太阳光可能需要8分钟才能抵达地球,对光而言却只是刹那。光穿越了时间的界限,瞬间可达宇宙任何角落,对于我们来说,才有所谓的光速概念。
答案一:由于光相对于其他参考系的速度为常量c,但若以光作为参考系,则需要考虑光的本质,两束光相对于时间静止,固有时为0,没有时间流逝,也就不存在速度概念,因此此问题无解。
答案二:顺带一提,关于同向问题,尽管无法进行计算,但我们可以举个例子。太阳光包含各种单色光,1666年牛顿通过三棱镜将其分解为多种颜色的单色光,它们同向且同时达到地球,因此同向的速度为0。

对于反向问题,若硬要一个答案,那应为无穷大。以两个光子为例,光子可以在瞬间移动至无限远距离,不受场干扰时,光子会沿着特定路径移动。由于方向相反,两无限远的距离相加即为无穷远。距离无限远意味着时间无限短,因此答案为无穷大。
