
浥尘社团高老师
我开了个号,叫“浥尘社团高老师”,想通过视频方式表达一下对现今教育、孩子们成长方面的个人见解和浅薄看法。
最近我聊到了关于将来,我们进入AI人工智能时代孩子们所需要重点学习的能力之一,就是数学能力。
我说的数学能力可不是一般人认为的解题和做题的能力,而是能将万物模型化、抽象化为数学公式定理的能力。
这种能力需要的是人的想象力和创造力,恰恰不是通过刷题式的方法能训练出来的。
它需要的是孩子们从小对大自然万事万物的亲密接触,在头脑里产生各种各样的立体的或多维的想象和记忆,从而可以将这些东西转换、模拟最终抽象化成普遍适用的数学模型、公式等。
这种将现实世界中的东西平滑地转换成我们头脑中的抽象物的情况,其实可以说是非常常见的。
不管是什么公式也好,还是什么定理也罢,都是这么来的。
举个例子吧!
我们在网上刷短视频,经常能看到有一种猜饮料的小游戏。
玩法并不复杂,找张桌子,在桌子下面放一上排不同品牌、不同颜色、瓶子形状也各不相同的饮料。
然后在桌子上面也摆上一排饮料,但是要与桌子下面放的数量相同,只是顺序不同。
当然,桌子下面的饮料是被遮住的,接着就让你通过尝试摆放桌子上面的饮料的不同顺序来猜是否与桌子下面的饮料顺序一致。
游戏期间有一名裁判,在每一轮摆放完成后,裁判会观察并提供给游戏者同时位置正确、饮料也一致的数量。
如果所有位置的饮料都摆放一致,则游戏胜利完成!
说了这么多,还是举个实际的例子比较直观。
比如,我这儿一共有三种饮料:可乐、雪碧、酸奶。
为了方便表述,我们将它们符号化,也就是用字母来表示。
可乐,用字母 A 来表示雪碧,用字母 B 来表示酸奶,用字母 C 来表示好,在桌子下面我们可以这么放:
A|B|C如果在桌子上面,我们这么放:
C|B|A那么摆对的数量就为 1 ,因为从左往右第二个,也就是只有中间那个位置的 B 是摆放正确的。
同样,如果桌子上面我们摆成了这样:
C|A|B那么摆对的数量为 0 ,因为一个也没对上。
好了,明白了吧?
游戏就是这么个规则,挺简单,也很有趣。
在网上这种视频中,参与猜饮料的玩家们也是热情高涨,参与人数不限,大人孩子都可以一起玩,真是非常棒的一款游戏。
组织这个游戏的成本几乎为零,非常方便啊,我们完全可以自己试着和孩子们玩一玩。
那么这么好玩的游戏,它到底是个什么原理呢?
怎么样才能又快又准地猜出正确的顺序呢?
如果孩子们能够提出自己的想法,并且能够进行思考,我觉得玩游戏是一个再好不过的方式了。
注意,我在这儿插句话,玩这类自然游戏是与手机游戏有很大的区别的,不可混为一谈。
好了,接下来我就现学现卖,假装做一名数学老师。
当然了,我对数学老师那是相当地尊重,所以像数学这种很有用的东西早早地就还给他老人家了。
废话不多说,我赶紧上网查了一下,原来这种猜饮料的游戏,其实就是数学中的“排列组合”问题。
你看,这就是将现实问题模拟抽象成数学问题,就是这么来的!
上过学的小伙伴们都应该学过“排列组合”吧!
什么?
你也还给老师了,嗯,好孩子!
没事,毕竟我们也只是和孩子们简单地谈一下有趣的数学,启发他们对数学的思考和兴趣嘛!
因此不会太过复杂,复杂了我也搞不定哈。
好,我们先把公式摘抄一下。
从n个不同元素取出m个元素的所有排列,公式如下:
A(n,m) = n!/(n-m)!从n个不同元素取出m个元素的所有组合,公式如下:
C(n,m) = n!/m!(n-m)!看到公式就头大吗,其实我们没有必要反感。
等会儿我只要告诉你们,这种令人讨厌的符号化知识是怎么来的,你们心里就会舒服多了。
好,可以先别管那些公式,我们眼么前只要先解决两个问题就行。
第一个,这个猜饮料的游戏,它应该是属于数学排列问题,还是数学组合问题?
不管排列还是组合,都是从一堆元素里取其一部分元素出来。
排列是指取出来以后元素还要讲究顺序,而组合就不讲究顺序了,只讲数量。
因此,我们就可以知道,猜饮料讲究的肯定是顺序,那它就是一个数学排列问题,而不是组合问题。
OK,第二个,猜饮料游戏中取出的元素是怎么确定的?
很明显,桌子上面和桌子下面的饮料数量都是相同的,所以按前面给出的公式,应该是从n中取出n个元素,也就是 n=m ,所取的饮料瓶数量就是总数量,对吧?
于是这个公式就可以变得超级简单了。
A(n,n) = n!你看,实际上它就是求n的阶乘。
啥叫阶乘?
就是某个数自己乘以自己减一,再乘以自己减二,一直乘以1为止。
n=n×(n-1)×(n-2)....×1比如 n 为 3 ,那么它的阶乘就是这样的,等于6。
3×2×1=6于是我们立马就能知道,这个饮料摆放的可能顺序和数量有关,并且可以计算出一共有几种顺序,就是饮料数量的阶乘数。
简单吧!
比如,桌子上一共三瓶饮料,那么它就有6种摆法,你算算对不对?
如果桌子上一共有四瓶饮料,那么它就有24种摆法。
我们用计算器,可以很方便地计算出阶乘。
先将计算器切换到科学计算模式。
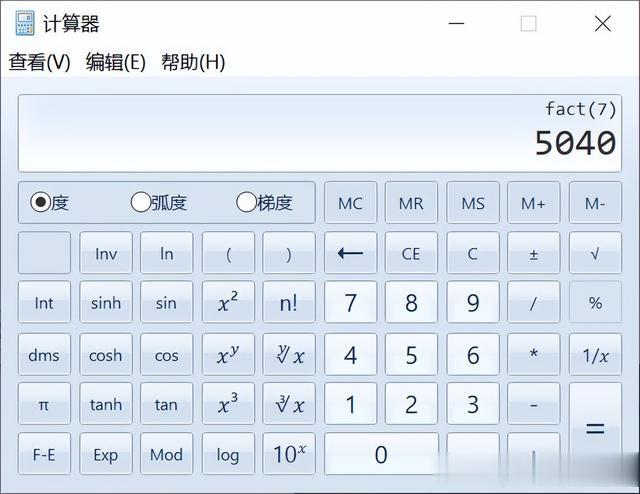
然后随便按个数字,比如 4 ,再按下 n! ,即可计算出 4 的阶乘为 24 。

如果你再算下去,你就会发现,7 的阶乘就已经达到了 5040 ,再往后数量级越恐怖。
这个阶乘计算是非常恐怖的,它让我想起了以前那个棋盘放米的故事,小伙伴们有兴趣可以自行查找。
因此,我们可以得出两点结论。
一,饮料游戏中的饮料数量不能太多,通常最多6瓶即可。
二,饮料数量越多,饮料可摆放的排列可能就最多,6瓶饮料就有多达720种排列顺序,够你摆上半天的了。
好了,说到这儿,关于猜饮料游戏,我们了解的已经不少了。
但是,怎么才能高效地猜出正确的顺序呢,这个问题有待研究。
于是我做了一个简易的模拟程序。

程序中我们可以先给出几个字母,来抽象表示不同各类的饮料,比如最简单的 ABC 。
然后点击“生成所有排列”,即可在右侧列表框中得到全部的排列。
想要玩一玩猜饮料游戏,那么就点击下面的“生成随机排列”,类似于在桌子下面摆放了一排饮料。
然后通过点击右侧列表框中的排列项,程序就会给出位置正确数来让你判断。
当然了,你可以增加饮料的数量,自然排列数也会陡增,玩起来难度会更大。

另外,使用英文字母来抽象表示事物并不是唯一选择。
你完全可以使用我们中国的天干地支,效果一样。
中国的古书上都是用天干地支来表达数字公式和描述定理的,只是我们现代人被灌输了西方思维,早已不习惯罢了。

如果你觉得怎么也猜不准,没关系,你还可以偷偷看一下桌子底下到底是怎么放的。

来吧,实际动手玩一玩吧!
网管小贾的猜饮料顺序游戏之数学排列演示程序
下载链接:https://pan.baidu.com/s/1ckMnWcwKZuQO2Pksjy4anQ
提取码:<关注公众号,发送001111>
感兴趣的朋友可以和孩子们玩一玩这个猜饮料的游戏。
同时也可以和孩子们探讨一下,数学到底是怎么来的,那些公式定理是从哪儿变出来的。
哈,其实就是我们在现实生活中,接触的各种各样有趣的事物,将它们抽象总结成公式和定理。
这种有很多哈,比如正弦、余弦其实是用来抽象表述太阳照射树木影子的变化。
还有前不久姜萍同学做的一道八音盒的竞赛题,都表明了数学是永远不能脱离实际现实的一门伟大科学。
然而我现在孩子们的学习,却本末倒置,先学抽象化的、符号化的东西,而抛弃了具体的、实在的东西,要是能学好才怪呢!
如果一个孩子能够学懂学好数学,那一定是他在自然世界中“玩”得足够多,这是毋庸置疑、无需争辩的。
最后,大家有空可以随时来看看浥尘社团高老师的视频,会随时给大家分享教育方面、孩子学习成长方面的内容。
希望能够对大家有所帮助,感谢大家围观!
