上次讲了SAR型ADC,这次讲最后一种,Σ-Δ型ADC。
4. Σ-Δ型ADC
Σ-Δ转换器又称为过采样转换器,其中Δ表示增量,∑表示积分或求和。与其他ADC不同的是,Σ-Δ型ADC不是直接对抽样数据的数值做量化编码,而是根据前后数值的差值(增量)做量化编码。由于不是对大的绝对幅值做编码,而是对增量编码,因此使用低分辨率的一位量化器就能满足要求。
组成:
Σ-Δ型ADC由两部分组成:简单的模拟电路(Σ-Δ调制器)和复杂的数字信号处理电路(数字滤波和采样抽取器)。以一阶Σ-Δ型ADC为例,它是由一个积分器,比较器,加法电路,时钟和开关等组成的模拟电路和数字信号处理电路组成。可以说,Σ-Δ转换器的数字特性多于模拟特性。示意图如下:

图1 Σ-Δ转换器原理图
工作原理:
1> Σ-Δ转换器是利用低分辨率的ADC(通常为1位)以及高采样速率(过采样)对模拟信号抽样并对增量进行量化,即得到数字Σ-Δ码。
2> 送入数字抽取滤波器进行噪声整形和数字滤波技术,提高数字信号分辨率。
3> 最后,通过采样抽取过程降低输出端的有效采样速率,去除多余信息。
与其他ADC相比,Σ-Δ型ADC本质上是一种以高速抽样率来换取高位量化,即以速率来换取分辨率的方案。
Σ-ΔADC的原理涉及到的三个概念:过采样(over sampling),噪声整形(noise shaping),数字滤波和采样抽取。
过采样:
根据奈奎斯特采样定律,我们知道当采样频率≥2输入信号频率时,才能保留原始数据的信息。当采样频率kfs>>2时,被称为过采样。
从频域上看,采样实际上是采样信号与输入信号和量化噪声做卷积,而采样频率越高,则频带越宽。因此当过采样时候,实际上是把输入信号和量化噪声进行了展频处理,而噪声的总功率不变的情况下,频谱扩展后,频谱密度就降低了。我们看图2,在奈奎斯特频率下采样,其中阴影部分为量化噪声,这时候加一个低通滤波器,则可把部分噪声滤除,但效果并不明显。图3则是过采样后加低通,长方形的量化噪声被展频了,但是密度低了,经过了低通后,滤除的噪声就会变多了。
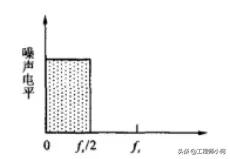
图2 奈奎斯特频率采样

图3 过采样
同时,过采样会降低后端模拟抗混叠滤波器的滚降要求。依据奈奎斯特准则,要求传输无失真,就要求滚降系数α越趋近于0越好,而越小则滤波器的设计难度越高。而过采样则会在前期就让数字滤波器将f/2到kf/2之间的量化噪声消除(k为过采样比),这样就把总信噪比提高了10log10(k)数字滤波器将fS/2和k*fS/2之间的量化噪声从输出中消除,其结果是总信噪比提高了相当于10log10(k)。即大概信噪比提高6dB(1位),过采样比高4倍,因此需要合理设计过采样比。
噪声整形:
噪声整形技术通常是指用差分电路(Δ)和累加器(Σ)设计电路,使量化噪声的频谱密度从原先的均匀分布转变成向高频段分布,如图3。经过整形后的噪声功率不变,但低频功率谱密度要比整形之前降很多。噪声谱经过调制器的整形之后,数字滤波器就可以消除大部分量化噪声能量,从而大幅提高总信噪比(以及相应的动态范围)。

图4 Σ-Δ调制后量化噪声
数字滤波和采样抽取:
这一部分是通过数字低通滤波器来完成的,经过Σ-Δ调制器后,噪声在f/2以内的几乎没有,这时候通过数字滤波器,则量化噪声中的高频部分就被消除了,只剩下了少部分的低频量化噪声。由于之前的过采样,使得频率提高,所以滤波后对数据进行抽取,将高速率低精度的数字信号转换成低速率高精度的数字信号输出。
优点:精度高,线性度好,对输入信号幅值变化不敏感,转换速率高于积分型和压频变换型ADC;由于过采样技术,抗干扰能力强。
缺点:高速Σ-Δ型ADC的价格相对较高;在转换速率相同的条件下,比积分型和逐次逼近型ADC的功耗高
应用:
由于过采样技术的应用,Σ-Δ型ADC对输入频率有要求,输入信号频率过高则会超过器件的极限频率。也因此,Σ-Δ型ADC主要用于高分辨率的中、低频测量和音频电路。
温度检测电路,由于精度高、采样率低的特点,Σ-Δ型ADC被广泛应用。
而由于Σ-Δ型ADC的动态范围较高,也广泛应用于数字音频电路中。
至此,ADC的四种经典类型原理及其应用已经介绍完毕,被人忽略的ADC系列也完结了。实际使用中还会碰到一些其他种类的,这里不再提及了。以后在实际工作中,碰到硬件调试的情况并不多见。但起码应该做到,见到应用场景,能反应出来是哪种ADC,有哪些需要注意的点。
