天文导航是最古老而基本的定位定向方式 , 以其精度高、隐蔽性好、可靠性高、自主性强等优势, 一直在舰船导航中占有重要地位。
国内外学者对其早有研究, 尤其在定位定向方面成果丰硕。美国已开发出三视场定位定向设备原理样机。
例如美国Trex公司已经开发出来多视场恒星跟踪器。它可以在白天, 位于海平面探测到6.3等的恒星, 并可完成定位定向或高精度姿态测量工作。此设备可以为航海提供精确的方位基准, 独立于惯性导航系统。

法国SODERN公司的HYDRA星敏感器, 也是三视场结构, 但它应用于航天器的姿态测量领域。 国内在天文定位定向方面最近三年的研究呈现多元化。
在原理上主要基于球面三角形原理的优化求解, 即通过天顶距、格林时角等建立球面三角形, 使用高度差的方法进行定位、定向,此方法不适合三视场定位定向的多误差源分析。
在定位定向设备方面多是基于单视场多次观测进行定位定向,尚没有多视场一次观测进行快速定位定向方面的研究, 且没有全面查看多种误差源对定位定向精度的影响。

对定位定向的误差研究主要是对求解算法本身的研究, 例如研究球面三角形优化方程的中高度角误差对定位结果的影响等。
文中首先说明定位定向的概念,给出基于解析几何法进行定位定向的原理模型。接着结合原理模型进行误差分析, 给出影响定位定向精度的误差源及其特性, 并建立定位定向误差模型。
然后,采用蒙特卡罗法分析误差源对定位定向精度的影响, 并指出哪些是主要误差源。最后, 通过实际实验验证了高精度定位定向的可行性以及影响定位定向精度的主要误差因素。
图1是三视场定位定向设备的结构框图。 它有三个光轴, 光轴可以在载体坐标系内定义。光轴的方位间隔为120°, 仰角均为45°。

图1 三视位定结构
定位主要是确定设备在WGS-84坐标系内的经纬度。 国际地球参考系和世界大地84坐标系基本上是一致的。 将一个地理位置标记为Loc, 其中海拔, 单位为m ; 经度、 纬度 φ, 单位为度。
由于海拔可由海拔仪测定 ;故定位在这里主要是确定经度、纬度。由 λ, φ, h通过公式可以获得位置在CITRS内的矢量表示, 简记为VLoc。
定向主要是确定图1中载体坐 标系CB在东北天坐标系内的方位角 , 将此方位角记作AziB。 图2给出载体方位角示意 , CB的XB轴在水准面ENO内的投影XB′ 与CENU的Y轴在水平面EON内的顺时针夹角, 即为设备待测量的方位角AziB。

图2 载体角
文中使用Rxyz表示旋转 矩阵 , 它的下标xyz表示旋转 轴及旋转 顺序 , Rx 、Ry 、Rz 是标准旋转矩阵, φx、φy、φz分别是旋转角。
在图2中建立辅助坐标系Ca: 其原点和CB的原点相重合, 其Xa轴沿着矢量XB′ 的方向 ;Za轴与CENU的U轴相重合;Ya轴符合右手定则。 由图2中可以知道坐标系Ca到CENU的转换矩阵满足下式:
在图2中 ρ、τ 是为水平倾斜角, 其单位为度。 其中 ρ 是单位向量XB′ 与单位向量XB的夹角; 而 τ 是单位向量YB′ 与单位向量YB的夹角, 且YB′ 与YB在水准面ENO内的投影相重合。 水平倾斜角由高精度的倾角测量传感器获得, 它在计算分析中是已知量。

图3是三视场天文定位定向设备的原理框图。定位定向信息对对完成定位定向十分重要, 它是三个视场内任意一个视场观测到的恒星分别通过计算和识别获得的, 阐述如下:
首先是通过系统固有参数计算获得星像在载体坐标系内的位置矢量。天体目标光线经过光学系统成像在探测器上面, 通过星图处理提取星像的质心位置 。
由质心位置、 焦距fc、 探测器像 元尺寸、 分辨率、 主点、 畸变参数、 光轴在载体中的单位矢量Axi Veci=[cos (Ai) cos (Ei) , sin (Ai) cos (Ei) , sin (Ei) ]T, 以及探测器安装角, 使用视觉几何的原理计算可得第i个视场内的星像在CB中的位置矢量VB, 如图2中所示 , 且满足下式 :
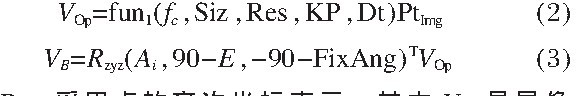
式中:PtImg采用点的齐次坐标表示, 其中VOp是星像在光学坐标系内的坐标。
图3 三视文定的原图
其次, 通过水平倾角和气象信息结合上述计算获取的 星矢量VB获得星矢 量在辅助 坐标系内 的观测矢量。 从坐标系CB到Ca之间的转换矩阵

与测量角 ρ 和 τ 相关, 简写为
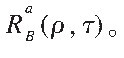
至此可得星像在Ca中的位置矢量:

矢量Via结合气象信息进行蒙气差校正后可得矢量Via。 此矢量是定位定向信息对的其中一项。
再次,通过任意视场星图中提取的质心计算获取其在CB内的位置矢量VB,并计算任意两颗星之间的星角距。 通过三角形识别算法识别出其为星表中编号p的恒星Starp。
然后,识别出的恒星Starp结合时间和极移获得星在ITRS坐标下的位置矢量。由世界协调时, 经天文计算可得Starp在真春分点赤道坐标系的位置矢量Vγ和格林威治视恒星时。GAST对应的角度记作AngGAST, 则恒星在地球过渡参考坐标系的位置矢量可由式计算 :

坐标系CTIRS至坐标系CITRS的转换与极移参数有关, 此参数可由国际地球自转和参考系服务处提供。可由下述公式6获取恒星在CITRS坐标系内的位置矢量,式子中xp, yp的单位为弧度, VITRS是星像在CITRS坐标系下的位置矢量:

此矢量是定位定向信息对的另外一项。
至此由某颗提取的恒星可以获得定位定向信息对

上标i表示不同的观测恒星 。
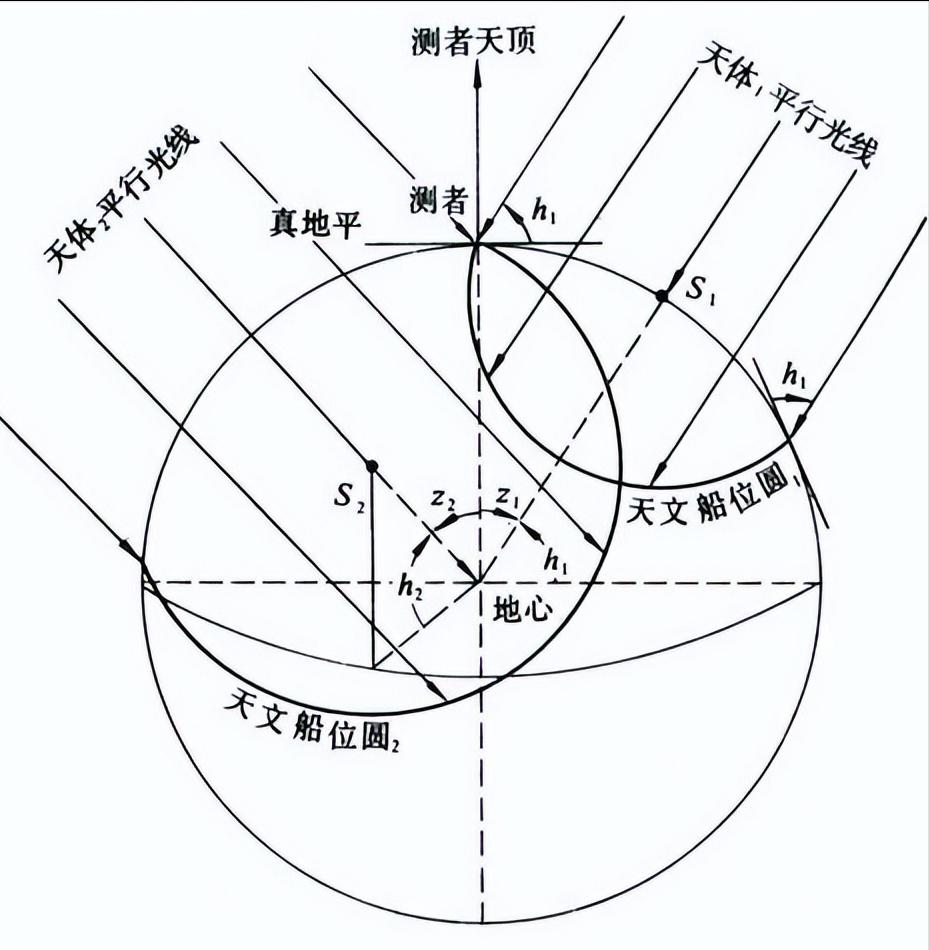
定位是由球面圆求交点的方式获得, 定向是在定位完成之后求解的。
由定位定向信息对

可以获得球面圆 ( 简记 Γi) 。 将矢量
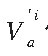
化为球面坐标系的量 αi, θi, RC表示, 其中 θi为与Za轴的夹角, αi是矢量
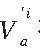
在 XOY的投影与X轴的夹角;而RC为天球的半径 , 单位为AU。 在坐标系CITRS中以ViITRS为轴, 以 θi为半径进行顺时针旋转, 获得一个旋转体, 此旋转体与天球的球面交线构 成一个球 面圆 , 记此空间 曲线为 Γi (ViITRS, θi) 。 在第二个视场中同样可由一颗恒星获取一个观测数据对, 构成球面圆 Γj (ViITRS, θj) 。 在CITRS内以RC为半径构建球面 Σ:

若点P= (xp, yp, zp) T是 Γi、Γj的交点, 那么P∈Σ, P∈Γi, P∈Γj。 向量OEP和Vi之间的夹角为 θi; 而向量OEP和Vj之间的夹角为 θj, 满足下式 :
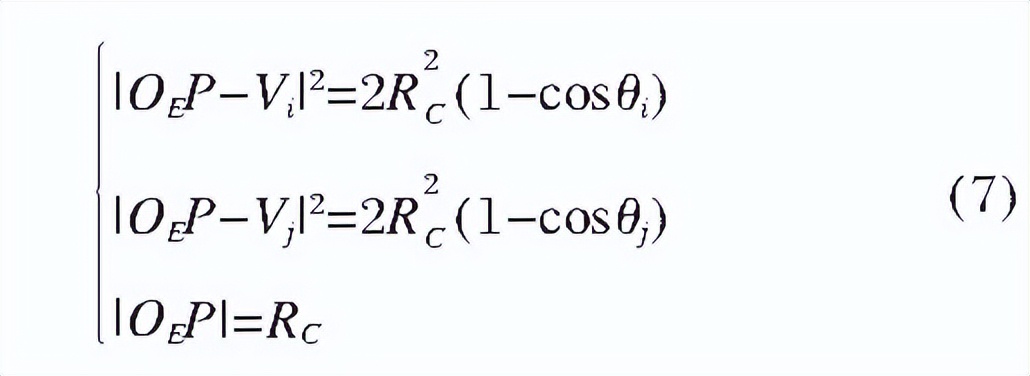
此方程有两个解析解分别为P0ij, P1ij, 其中上标为0的是真解 , 为1的是伪解 ; 下标ij表示不同视场内编号为i、j的观测数据对。
由第三个视场内的识别恒星可获得第三个球面圆 Γk。 此时三个球面圆可获得6个交点 。 若观测矢量Va′ 没有引入误差 , 那么这6个交点中3个是相等 , 此点就是真实的解, 即
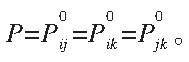
通过P点可获得向量OEP以及单位矢量

将
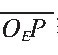
转换为球面坐标系可获取天文经纬度 (Λ、Φ) 。
实际上观 测矢量Va′ 会引入误差。当观测到2N ≥3个定位定向信息对时 , 可获得N (2N -1) 个代表真实解的交点。 求取P点的问题可以转换为求下述函数G0最小值的问题:
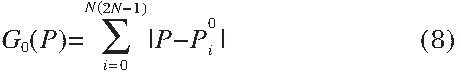
公式8可以转化为求取G1最大值的问题:

它是带约束条件的二维函数求最值问题, 可用拉格朗日的方法求解。 求取公式9的最大值就可以求得点P, 进而求取到优化的天文经纬度 Λ、Φ。
求天文经纬度 Λ、Φ 之后, 对任意定位定向信息对{VITRS, Va′} 结合下式可得信息对 {VENU, Va′} :
由于
故公式 (10) 可以简化为 :

由于{VENU, Va′} 结合公式1可得 :

式中:仅有一个未知数AziB, 故可以直接求得 。 当有多个定位定向信息对时, 求取AziB的均值作为定向的优化值。
天文经度纬度区别与地 理经纬度; 且天文学上的定向结果AziB与地理学上的定向结果Azi′B不同, 这是由于垂线偏差造成上。在WGS84坐标系内将垂线偏差的两个分量记作η, ξ, 单位为度 , 它可以由地理数据共享平台离线获取。 天文经纬度和地理经纬度的关系如下:

而地理定向的结果可由下式得出:

至此, 真正完成了地理学上的定位和定向。
在完成定位定向过程中, 需要获取时间、水平倾斜角、气象数据、恒星质心;并且还需要知道设备标定的固有参数:光学系统 内参数 、三个光轴 在CB内的位置矢量、CCD安装旋转角。在精确计算时需要极移数据, 但其不可能实时获取;垂线偏差数据是由第三方数据库获取的数据, 其自身也存在模型误差。

图6 定位的仿
这些误差都将引入计算过程中, 最终对定位定向的结果造成误差影响。除垂线偏差外, 其他类型误差均是对定位定向信息对造成影响, 进而影响到定位定向结果。
国内的张圣云等给出定位定向精度分析中仅仅定性地分析给出水平测量精度越高 , 定位精度更高;没有探讨对定向精度的影响;更没有建立误差分析模型分析各种误差源对定位定向精度的影响。
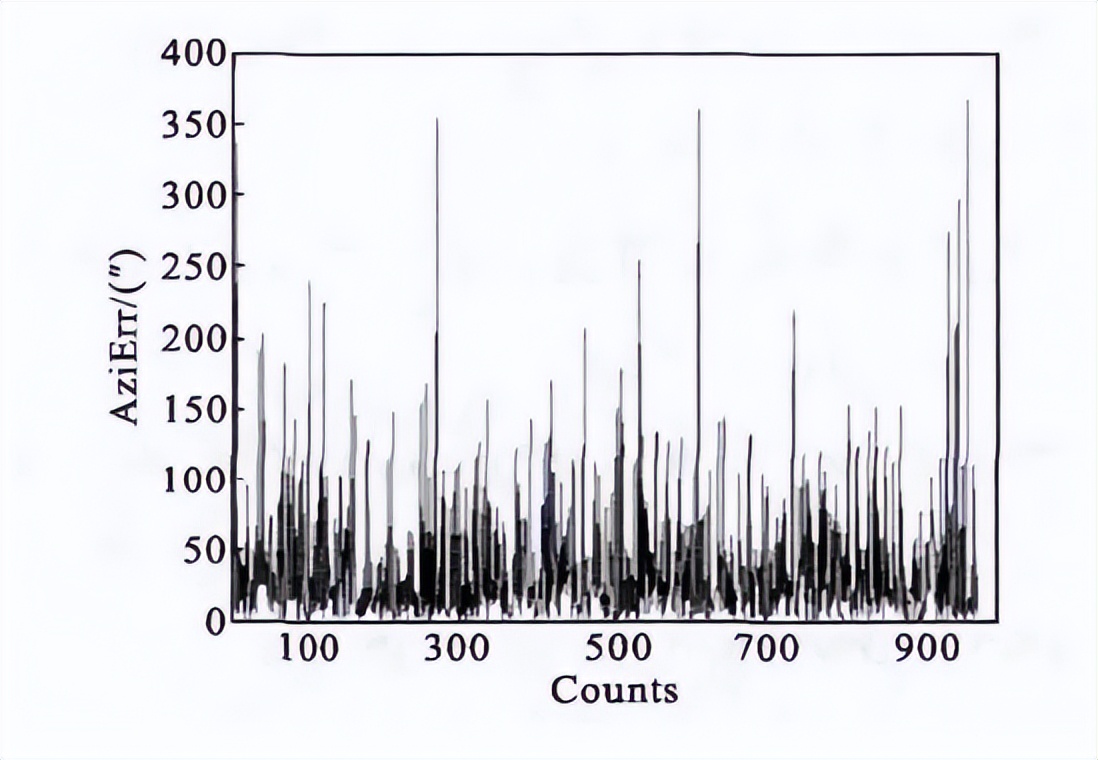
图7 定向的仿
国外的三视场定位定向研究中也并未对误差源做全面的数值分析,而是直接给出产品 。
在之前定位定向研究中多是基于高度差进行天文定向分析。均未对垂线偏差、极移误差、大气折射等误差对定位定向的影响大小做出探讨。
其定位定向过程中并未考虑重力场异常对定位定向数值影响的大小 , 而是建立在理想情况下进行分析的。之前的定位定向研究中由于没有使用垂线偏差数据库, 最后的定位定向结果多是天文学意义上的定位定向;

表2 单独添加各组误差时定位误差的仿真结果
即使是少部分学者测量出实验地点的垂线偏差数据, 进行了地理学上的定位定向实验, 但最后并未分析垂线偏差数据在整个地球范围内对定位定向精度的影响。
据表1中给定的各个误差源, 首先添加所有的误差进行综合仿真分析, 给出在所有误差源影响下的定位定向精度。然后分别单独添加各个误差源, 测试分析独立的误差源对定位定向结果的影响, 并给出对定位定向误差起主要作用的误差源。
在综合分析所有误 差源对定 位定向影响时 , 对于水平 倾角传感 器的测量 误差采用 单轴标准 差为0.001° (±3°) , 其他数据如表1所示 。图6和图7给出了定位定向误差的仿真结果。 图6中定位误差的均值为121.0 m, 平均偏差 为53.0 m;图7中定向误 差的均值为7.4″, 平均偏差为6.1″。

表3 单独添加各组误差时定向误差的仿真结果
将表1误差分为如下6组, 它与表1中编号对应关系 如下 : Ⅰ水平倾角 传感器测 量误差——— (1、 2) 、Ⅱ 质心提取误差 ——— (6) 、Ⅲ 光学系统标定参数的误差——— (7、8) 、Ⅳ气象参数测量及蒙气差校正的误差——— (3、4、5、B) 、Ⅴ忽略极移 的误差——— (9) 、Ⅵ垂线偏差数据自身的误差——— (A) 。 仿真过程中添加的水平倾角传感器单轴标准差为0.001° (±3°) , 其他数据如表1所示。
由表2可以看出定位精度受水平倾角传感器的测量误差影响最大, 垂线偏差数据库中的自身数据误差对定位精度的影响位居其次。由表3可以看出, 水平倾角传感器的测量误差对定向精度影响最大 , 光学系统参数标定误差引起的定向误差位居其次 , 但垂线偏差数据的误差引起的影响也较大。

表4 不同水平倾角测量误差时定位定向误差的
针对水平倾角传感器器测量误差影响最大的特点, 表4给出在不同单轴测量误差时定位定向误差的仿真结果。由表可以看出随着单轴测量误差的增加, 定位定向误差急剧增加。
质心提取的误差对定位定向造成误差的影响不是很大。 针对三种不同的质心提取精度, 表5给出仿真结果。由表5可以看出质心提取精度对定位定向的影响不是特别大。
由上述的仿真分析可以得知, 水平侧倾角的精度对定位定向的影响最大, 选用高精度的水平倾角测量设备或者高精度的水平测量方法是关键。

文中首先阐述了天文定位定向的概念, 并给出了三视场天文定位定向系统的工作原理。 提出了一种三视场导航系统基于解析几何法进行定位定向算法, 该算法能够同时解算地理位置和载体方位角信息。
接着分析了影响系统定位定向精度的误差源及其特性, 建立了定位定向误差分析模型, 采用蒙特卡罗法进行误差分析。然后仿真分析得出:载体平台倾角测量误差是定位定向误差的主要来源, 垂线偏差对定位定向的影响也十分显著。
若要进一步提高定位定向的精度, 则需要采用更高精度的水平倾角传感器, 提高水平测角的精度;另外就是使用误差更小的垂线偏差数据库。 最后进行了外场实验,结果表明使用文中算法的三视场天文定位定向系统的定位精度为182.12 m, 定向精度为9.3″, 可以实现较高精度天文定位定向。
