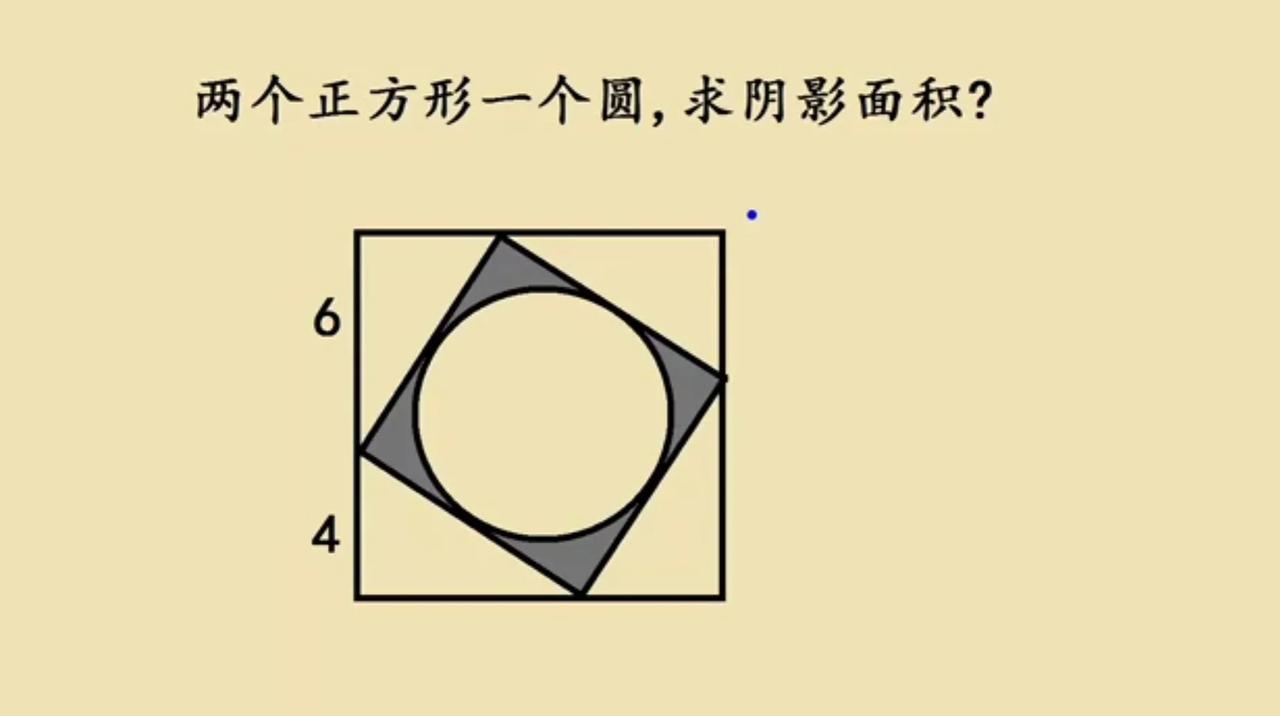
广州名校一道小升初考试压轴题，真正能拉开大家分数的几何题目，正确率不到10%！ 如图所示，两个正方形一个圆，求阴影部分面积？ 这道题关键就是利用面积关系，小正方形面积可以借助面积差而圆的面积又和小正方形面积存在关联，你会吗？
这是一道小升初考试题，多年前的一道附加题，不愧是压轴题，非常考验学生的基础知识和
【3评论】【1点赞】
广州名校一道小升初考试压轴题，真正能拉开大家分数的几何题目，正确率不到10%！
大力小学数学吖
2025-02-10 11:27:01
0
阅读：237
用户11xxx22
52-13兀
用户10xxx48 回复 02-10 17:00
赖东生
要计算阴影面积，我们需要了解图形的具体排列和尺寸。根据文件内容，我们有两个正方形和一个圆，但没有提供具体的图形排列方式和尺寸。假设两个正方形的边长分别为6和4，圆的直径与其中一个正方形的边长相同。 1. **假设排列方式**：假设两个正方形和一个圆排列在一起，其中一个正方形的边长为6，另一个为4，圆的直径与边长为6的正方形相同。 2. **计算正方形面积**： - 大正方形面积：\(6 \times 6 = 36\) - 小正方形面积：\(4 \times 4 = 16\) 3. **计算圆的面积**： - 圆的半径：\( \frac{6}{2} = 3 \) - 圆的面积：\( \pi \times 3^2 = 9\pi \) 4. **计算阴影面积**：假设阴影面积是两个正方形面积之和减去圆的面积。 - 阴影面积：\(36 + 16 - 9\pi = 52 - 9\pi\) 因此，阴影面积为 \(52 - 9\pi\)。如果需要数值结果，可以代入 \(\pi \approx 3.1416\) 进行计算。
濂溪子
240-60π
JYYX
简单得出奇啊