“很有挑战性,难度不小!”小学六年级数学拓展题:梯形内局部图形面积已知,咋求整体面积?主要考查“等高三角形面积面积比等于底边之比”! 如图,在梯形ABCD中,G为BD上一点,AG⫽CD,三角形ADG和ABG的面积分别为12和24,求梯形ABCD面积。 解题关键点或突破口:AG⫽CD! 难点:示意图未将AG延长并与下底BC相交!若此,难度将下降不少! —————————— 提示:等高三角形面积比等于底边之比(特别地,同底等高三角形面积相等)! ①延长AG、与BC相交于点E,连接DE,则ADCE为平行四边形,S平行四边形ADCE=2S△ADE。 ②S△ADE=S△ABD=36,从而S△DEG=S△ABG=24,S平行四边形ADCE=36×2=72。 ③S△BEG/S△DEG=BG/DG=S△ABG/S△ADG=2,从而S△BEG=2S△DEG=48,S△ABE=72。 友友们,怎么看?欢迎留言分享!
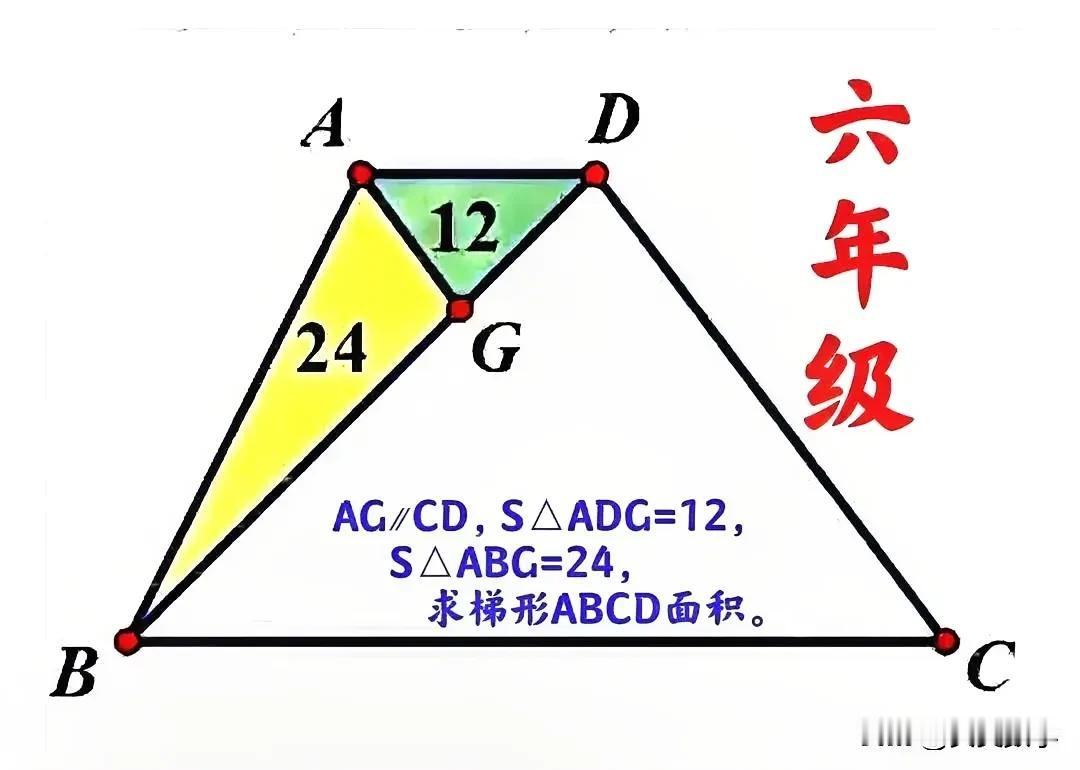




延长AG、与BC相交于点E,平行四边形AECD2倍于△ABD=72 △ADG∽BGE且高度1:2,故BGE=48 48+36+72=156
132?