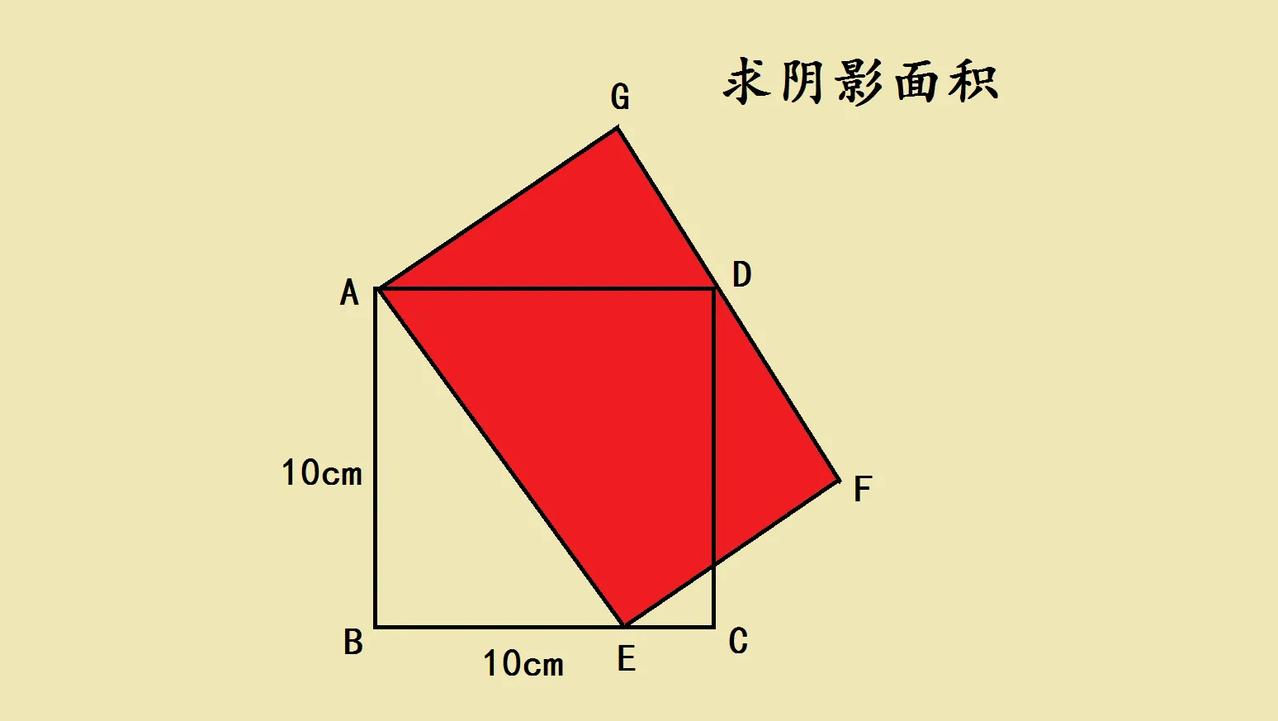
这是一道小学五年级附加题，不少学生抱怨题目给出的条件不充分，无法计算阴影部分面积。 如图所示，正方形的边长是10厘米，求阴影部分面积？ 我们需要找到正方形和长方形面积关系，可以通过“桥梁”把二者想办法结合起来。
这是一道小学五年级附加题，不少学生抱怨题目给出的条件不充分，无法计算阴影部分面积
评论列表
知识百科
- 1 乳汁的结构是什么
- 2 驾役怎么念
- 3 顺风使帆相关词语是什么
- 4 少年行诗句有哪些
- 5 瓜田之嫌繁体是什么
- 6 蜗跧的结构是什么
- 7 野服怎么读
- 8 中国电信10000周末打不通
- 9 激伶的结构
- 10 牛全价饲料主要成份是什么
热门分类
100？
用初中相似△可知：△ABE∽△ADG∴AE：AD=AB：AG即AE*AG=AB*AD=10*10=100
连接DE，可证△ADE＝1/2正方形ABCD，同理，除△ADE外的阴影部分面积亦可证＝1/2正方形ABCD，所以面积为10×10=100
不需要证明相似三角形，连接DE，就知道答案了！即S△ADE=1/2正方形面积=1/2长方形面积，∴长方形面积=正方形面积=10*10=100cm²。
一般这种题就是两个图形一样的面积，所以有百分之五十几率答面积一样能得分，不会的同学就按明面的写，比白卷好
连接D E,S△ADE是正方形面积的一半，也是印影面积的一半，所以10×10÷2×2=100
啥都不用做，直接硬干更简单，长方形边长AG=10*Cos∠GAD, 另一个长边AE=10/Cos∠BAE, AE*AG消去余弦得100[并不简单]