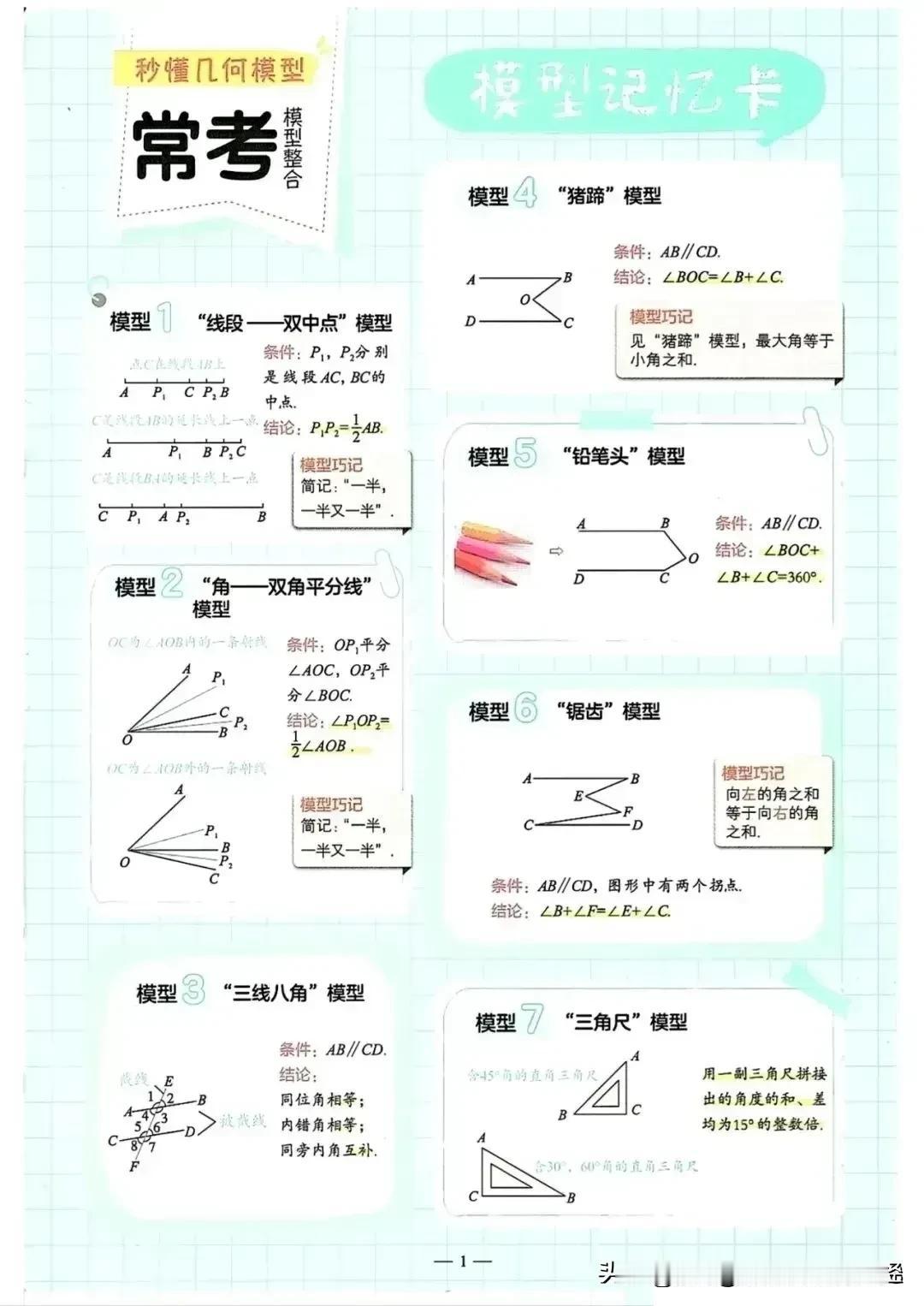
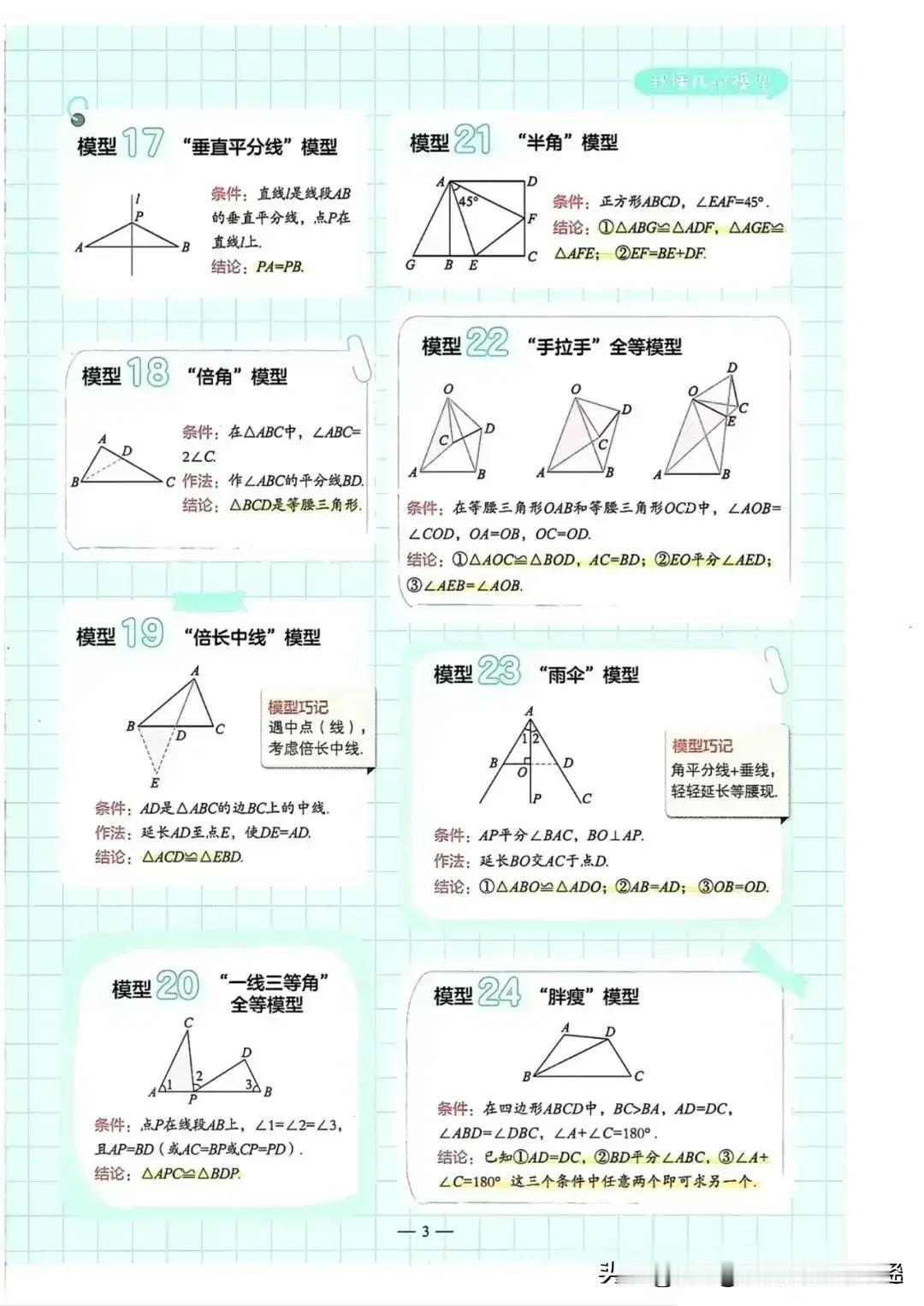
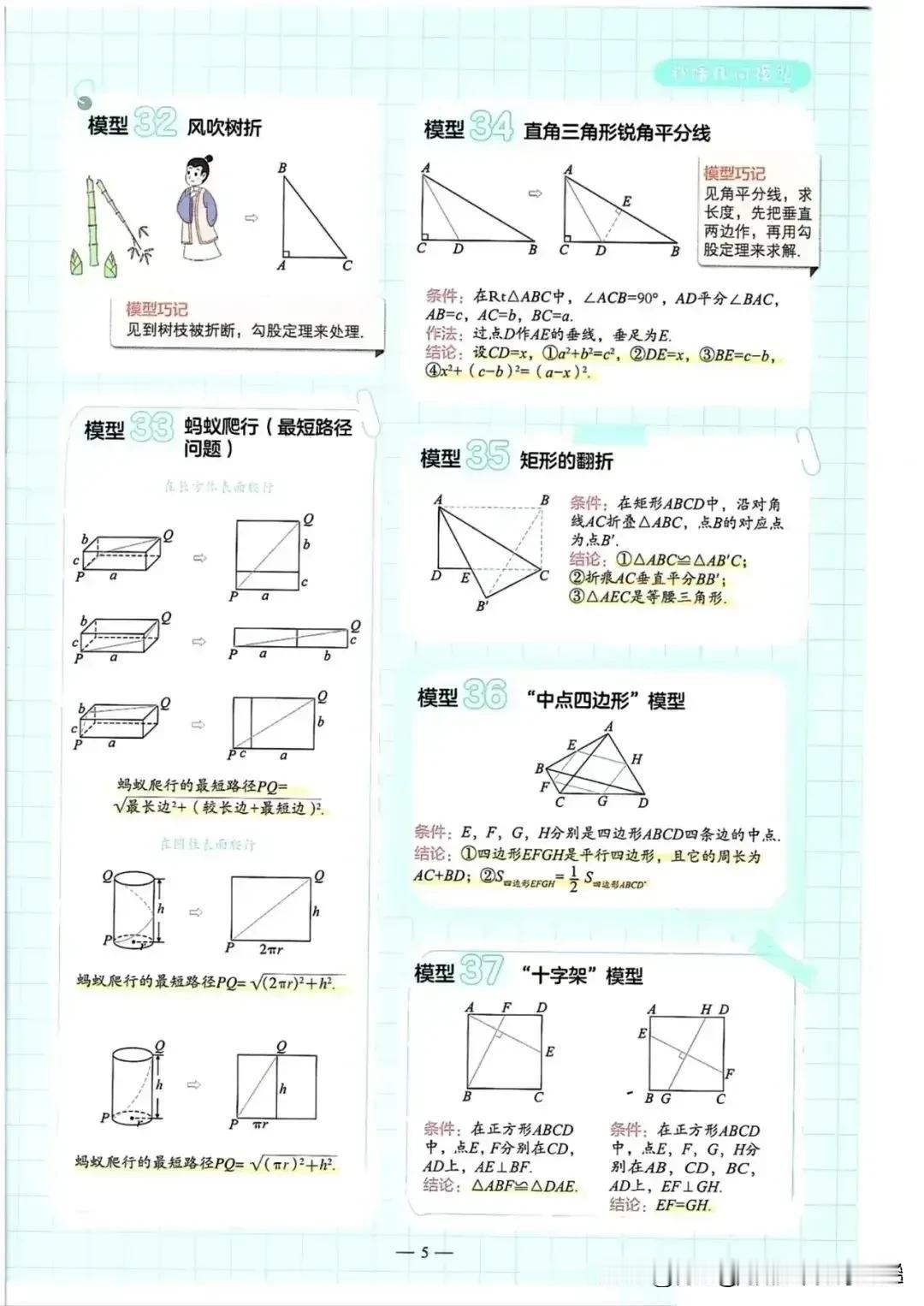
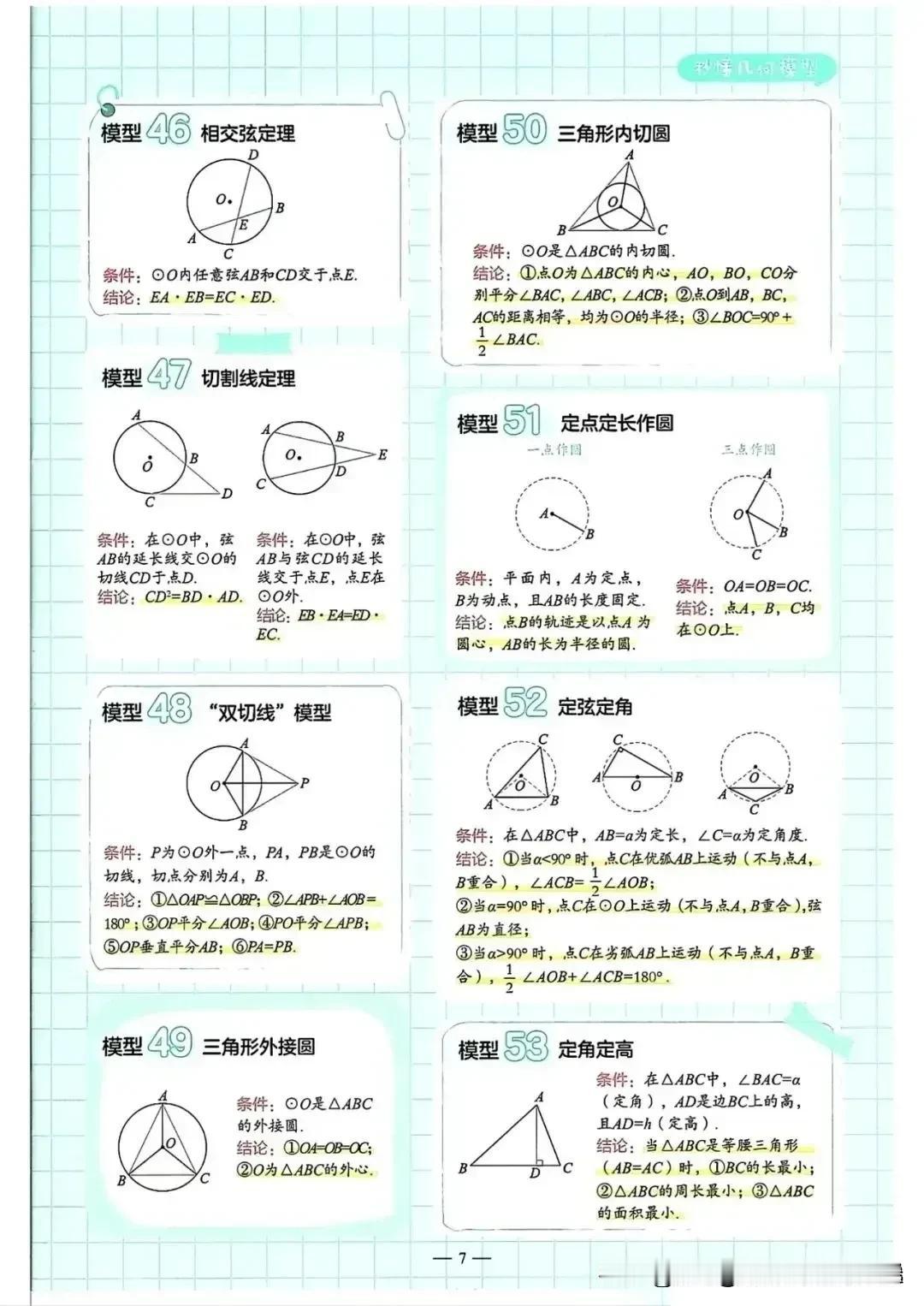
据说一位衡水10年班主任肺腑坦言：“几何”是初中数学最难教、学生难学的知识点，几乎没有啥规律，但是令人相见恨晚的是，班主任整理出来61个常见几何图形，看完后真的被惊艳到了，是鸡娃道路上的巨大助力，替孩子存下来！ 那么，什么是几何辅助线呢？简而言之，辅助线是为了简化复杂图形、揭示图形间的内在关系而人为添加的线段或图形。它们虽非题目本身的一部分，却是打开解题思路的金钥匙。 例如，在遇到直角三角形时，若需证明两线段相等，可以考虑通过构造斜边上的中线，利用中线性质（中线等于斜边的一半）来简化问题；在遇到平行四边形时，若需证明两角相等，可以通过连接对角线，利用平行四边形的对角线性质（对角线互相平分）来找到解题的突破口。 为了帮助学生克服几何难题，这位班主任不辞辛劳，整理出了61个常见的几何图形及其对应的辅助线技巧。 示例一：三角形中的辅助线 问题：在ΔABC中，AB=AC，AD是中线，求证AD平分∠BAC。 辅助线添加：连接BD并延长至点E，使得DE=BD，连接AE。 讲解： • 通过延长中线BD并构造等长的DE，我们得到了一个新的三角形ABE。 • 由于AB=AC且AD是中线，根据等腰三角形的性质，我们知道BD=CD。 • 由于DE=BD，因此AE=AD=DC（因为AD=BD+DC/2，且DE=BD，所以AE=BD+BD=2BD=2×DC/2=DC）。 • 接下来，我们可以证明ΔABE≌ΔACD（SAS），从而得出∠BAE=∠CAD。 • 因为∠BAE和∠CAD是∠BAC的两个部分，所以AD平分∠BAC。 示例二：平行四边形中的辅助线 问题：在平行四边形ABCD中，E、F分别是AB、CD的中点，求证EF∥AD且EF=1/2AD。 辅助线添加：连接AC，交EF于点G。 讲解： • 由于ABCD是平行四边形，所以AB∥CD且AB=CD。 • E、F分别是AB、CD的中点，所以AE=CF。 • 由于AE∥CF且AE=CF，我们可以得出四边形AECF是平行四边形。 • 在平行四边形AECF中，对角线AC、EF互相平分，所以G是AC的中点。 • 由于G是AC的中点且E是AB的中点，根据三角形的中位线性质，我们知道EG=1/2BC。同理，FG=1/2DA。 • 由于ABCD是平行四边形，所以BC=DA，因此EG=FG。 • 又因为EG和FG都与AC平行（因为它们都是AC的一部分或延长线），所以EF（EG+FG）也与AC平行。 • 由于E、F是AB、CD的中点且ABCD是平行四边形，所以EF=1/2(AB+CD)=1/2×2AD=AD（但注意这里的EF实际上等于平行四边形的一组对边的一半之和的一半，由于平行四边形的对边相等，所以EF=1/2AD）。 这里的直接推导EF=1/2AD略去了中位线性质的直接应用，更严谨的推导应基于三角形AEG和CFG与ΔABC的相似性，得出EG和FG分别为ΔABC两边的一半，从而EF为AC的一半，再结合平行四边形的性质得出EF=1/2AD。 示例三：梯形中的辅助线 问题：在梯形ABCD中，AD∥BC，∠B+∠C=90°，E、F分别是AD、BC的中点，求证EF=1/2(BC-AD)。 辅助线添加：过点E作EG∥AB交BC于点G，过点F作FH∥CD交AD的延长线于点H。 讲解： • 由于AD∥BC且EG∥AB，所以四边形ABGE是平行四边形。根据平行四边形的性质，我们知道AB=EG且AE=BG。 • 同理，由于FH∥CD且AD∥BC，所以四边形CDHF也是平行四边形。因此，CD=FH且CF=DH。 • 由于E、F分别是AD、BC的中点，所以AE=ED且BF=FC。结合前面的结论，我们可以得出BG=ED且CF=DH=1/2(BC-BG-FC)=1/2(BC-AD)。 • 由于∠B+∠C=90°，且EG∥AB和FH∥CD，所以∠EGC=∠B且∠CFH=∠C。因此，∠EGC+∠CFH=90°，即∠GFH=90°。 • 在直角三角形GFH中，由于G、F分别是BG、CF的中点（且BG=ED、CF=DH），所以EF是斜边GH的中线。根据直角三角形的中线性质，我们知道EF=1/2GH。 • 由于GH=GC+CH=GC+DH+HD=GC+CF+ED=BC-BG+ED=BC-AD（因为BG=ED），所以EF=1/2(BC-AD)。 这些图形涵盖了直角三角形、平行四边形、梯形、圆等几何学习的重点与难点，每一种图形都配以详细的解析与辅助线示例，家长保存收藏起来给孩子看看，更多几何辅助线可以系统学习下，帮助学生通过直观感受，掌握辅助线的添加原则与技巧，从而突破解题瓶颈，提升解题效率。 中考几何辅助线技巧