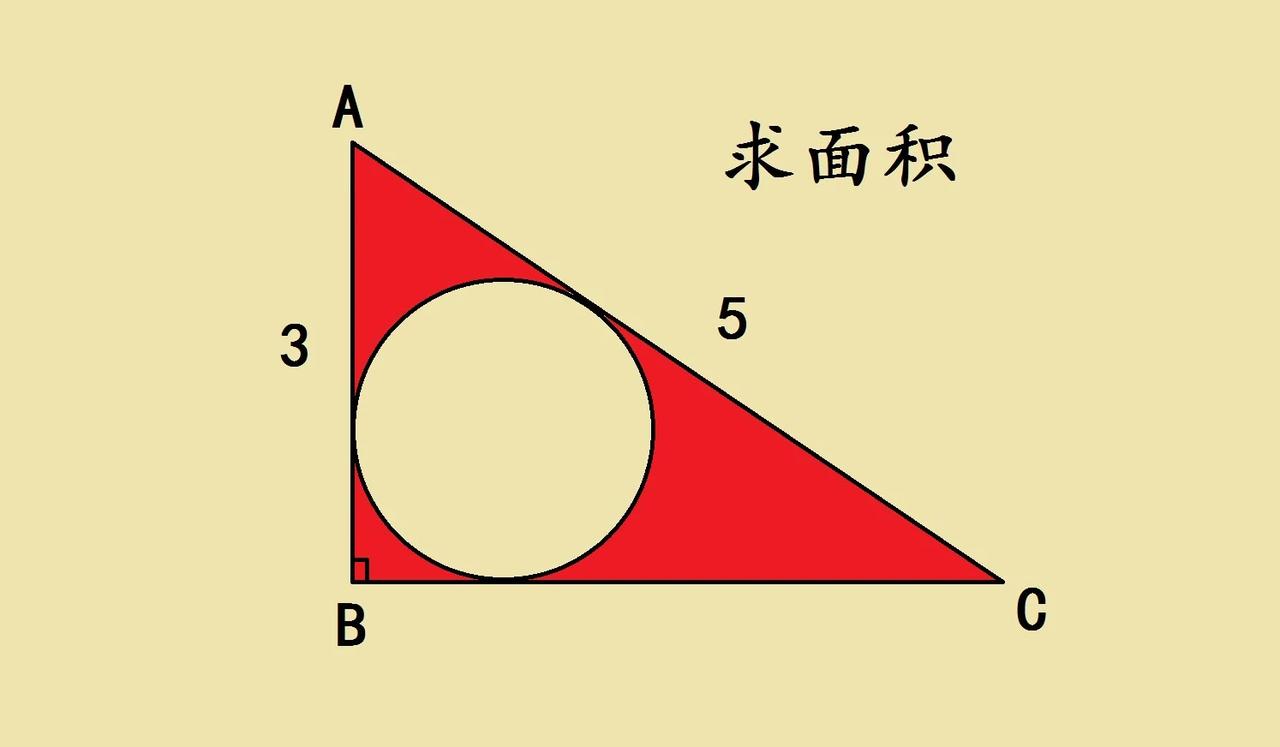
小学六年级几何竞赛题，难度非常大，经典的求面积，很多学生被难住了。 如图所示，直角三角形直角边是3，斜边是5，内有一个圆相切，求阴影部分面积？ 我们可以利用面积差，通过直角三角形和圆相切的关系，考虑圆心和切点连接，构造多个直角三角形然后利用面积法求解。
小学六年级几何竞赛题，难度非常大，经典的求面积，很多学生被难住了。 如图所示，
大力小学数学吖
2024-09-13 12:37:29
0
阅读：312
小榔头007号
利用三角形全等得(3-r)+(4-r)=5，r=1
o舞ooo舞o
先作辅助线，圆心到三个切点，然后三个三角顶点到圆心。用相等三角形公式证明A到圆心C到圆心切出两个相等三角，得出3-r+4-r=5，得r=1
OSLake
根据勾股定理算出BC长度，连接圆心到各切点，分割乘三个三角形，高为半径r：3r/2+4r/2+5r/2=3*4/2
人公
3+R＝4，R＝1
(神算子)梦入神机
这个必须用勾股定理
流水哥哥
设ab=x+y=3,ac=x+z=5,bc=y+z=4,2（x+y+z）=12, x+y+z=6 x=2,y=1,z=3 至于圆的面积自己算吧！
喂，是你
6-π
用户10xxx48
6-π
用户11xxx23
用到勾股定理，三元一次方程和完全平方公式，严重超纲了