自从孩子问起导数这个问题，最近研究了下，高中阶段的确引入了导数，可能一部分孩子一时难以接受这个概念。根据个人理解，通俗的谈谈这个导数的理解，希望有助于孩子理解入门。

其实吧，导数就是一个数学工具。可以把它想象成“瞬时速度”或者“斜率的变化”。想象一下，你正驾驶在一条笔直的高速公路上，速度稳定在每小时60公里，这时候的“速度”，就像是一个平稳的呼吸，不急不缓。但突然，你踩下了油门，速度飙升，或者轻踩刹车，速度渐缓——这一刻，“速度的变化”，正是导数在生活中的缩影，它捕捉着每一刻的加速与减速，如同记录时间轴上位置的微妙跳动。

在数学的奇幻世界里，y是梦想的彼岸，x是探索的航程。想知道这段旅程是悠然漫步还是疾驰如风？那导数就可以来揭秘，它就像一台精密的测速仪，测量着y随x每一步的“心跳加速”或“温柔放缓”。

导数就像是微观世界的侦探，它潜入函数某一点的附近，捕捉自变量那几乎看不见的微小变动，然后计算这变动下函数值的反应。当变动趋近于无，得到的极限值，就是那一刻的“变化率”——导数的真身。

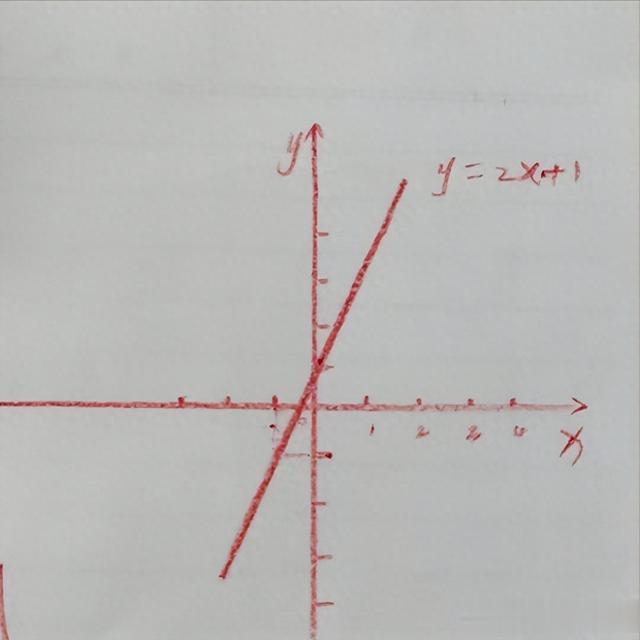
想象一下，你站在函数y=2x+1的图像上，目光锁定在一个点上。现在，慢慢靠近，再靠近，但不要触碰，就像欣赏一幅画作的细节，你会发现，无论你怎么移动，y总是以2的步伐与x同步起舞，这就是线性函数的“均匀心跳”，导数恒为2，简单而纯粹。

但当函数变得复杂，比如y=x²，导数的面孔就丰富了起来。它不再是那个一成不变的数字，而是随着x的起伏，展现出不同的面貌。x=1时，它是2；x=2时，它跃升为4……每一次x的跳跃，都带动着导数的新篇章，绘制出函数值变化的快慢图谱。

导数在实际应用中的一个典型例子是物理学中的“速度”和“加速度”概念。高中阶段物理会学到的。

想象一辆汽车在行驶，它的位置随时间的变化可以用一个函数来表示，比如s(t)表示t时刻汽车的位置。那么，这辆汽车的速度v(t)实际上就是位置函数s(t)关于时间t的导数，即v(t) = s'(t)。

速度本身也可以是一个变化的量，比如汽车可能在加速或减速。那么，加速度a(t)就是速度函数v(t)关于时间t的导数，即a(t) = v'(t) = s''(t)。

现在，假设一辆汽车从静止开始，以恒定的加速度启动。它的位置函数可以表示为s(t) = 0.5 * a * t^2（这里a是加速度，t是时间）。

求速度：

对位置函数求导，我们得到速度函数v(t) = s'(t) = a * t。这告诉我们，在任何时刻t，汽车的速度都是加速度a与时间t的乘积。

预测未来位置：

如果我们知道汽车的加速度a和它在某个时刻t0的速度v0（也就是t0时刻的导数v(t0) = a * t0），我们就可以预测它在未来任何时刻的位置。只需将速度函数积分回位置函数，并代入初始条件（比如t0时刻的位置和速度）即可。

解决实际问题：

在实际生活应用中，我们可能会遇到这样的问题：一辆汽车从静止开始加速，经过一段时间后达到了某个速度v。我们需要计算它在这段时间内行驶了多少距离。这可以通过对速度函数（即加速度的积分）进行积分来得到位置函数，并代入初始条件和最终速度来求解。

导数在这个例子中的应用不仅限于速度和加速度的计算，它还帮助我们理解了函数（在这里是位置、速度和加速度）之间的关系，以及如何通过已知的信息来预测未来的状态。其实这种预测能力在物理、工程、经济等许多领域都是非常重要的。这或许就是高中开始引入导数的原因，通过这个学习，可以筛选出一部分能力强的孩子进入大学深造。