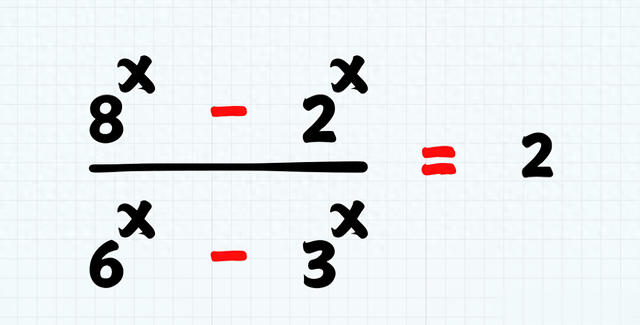
没有两个数字满足这个等式;通过检查,你可以找出满足这个等式的单个数字。
许多人在遇到这个问题时可能会考虑的一种方法是交叉相乘。但这种策略可能会导致复杂情况,并可能让你走进死胡同。
挑战在于,假设x是一个整数,找到x的所有可能值。
你会用什么方法来解决这个问题?
提示:表达分子和分母,使得它们有一个共同的因子,可以抵消它,从而得到一个不太复杂的等式。
拿起笔和纸,尝试一下。我很想在评论中看到你的方法。如果你做对了,就击掌!但如果做错了,也不要着急——跟着做就行了。
如果这个挑战引起了你的兴趣,请查看下面的其他谜题列表!
你准备好了吗?让我们开始吧!
仔细看看等式的左边。我们可以从分子和分母得出一个共同点。
我们开始吧!
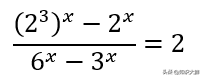
伟大的!
我们再做一件事。

太棒了!我们可以看到2^x是等式中非常常见的项。这告诉我们可以继续进行因式分解。
分解因式后,我们得到:

仔细观察;我们可以将 ( 2^x)²-1转换为两个平方差的表达式。

太棒了!你在想什么?
现在分子和分母中都有一个共同项。让我们将其抵消吧!

这给我们留下了:

伟大的!
此时,我们可以通过交叉相乘得到线性表达式。

让我们除以 2。结果如下:

太神奇了!还有一件事。仔细看看这个等式,任何大于或等于 2 的值都会使这个等式无效。为什么?
左侧永远是 2 的因数,这意味着它永远是偶数。另一方面,无论x的值是多少,右侧永远是奇数。
任何等式要想成立,等式的两边都必须是奇数或偶数。
请记住, x的值是整数。这也意味着任何小于或等于 -1 的数字都不满足该等式。
我们还剩下哪些范围的价值观?

0,显然不满足方程。
那1呢?让我们看看!

太棒了!我们找到了!1是唯一满足该等式的整数。
