01
荡秋千
说到荡秋千,一定能勾起大家的儿时回忆,但这项看似再简单不过的童年活动,其实是充满了技术含量的!荡秋千容易,但是怎样才能像歌词中唱的那样“荡到天外天”呢?
很多人第一反应可能是:找个人在后面推自己呀!正所谓芳园四壁花光闻,秋千动处朝霞飞。在春和景明,万物复苏的时节,和自己的男/女朋友一起荡秋千,想必是欢声笑语,浪漫之至。而这正是物理学中共振的原理呀!在秋千的每一个摆动周期我们都施加一次外力驱动,因此外界的驱动频率与系统本征频率接近,产生了爱的共振,所以我们才能将秋千越荡越高。

这种方法虽然浪漫,但却有着很大的限制,那就是:没对象的话怎么办呢?
难道我们单身狗就不配荡秋千了吗(摔)
其实即使自己一个人,我们也是能把秋千荡起来的,方法就是今天我们要介绍的“参变振荡”。具体操作如下所示:

如左图所示,当秋千到最高点时突然蹲下,然后到最低点时再突然站起来,那么人体重心的变化就如右图中A→B→C→D一样。在最低点我们要克服重力做功,将人体内能转化为机械能,由于B点与C点之间的高度差,所以D点高度是一定大于A点的。从D点开始再次迅速蹲下开始下一个“蹲→起→蹲”的周期,循环往复下去,我们单身狗就也能够“荡到那天外天”啦!

当然了,现实生活中很多秋千为了安全或舒适起见,设计为了只能坐着荡,这个时候我们也是有办法的,如下图所示:

不好意思,放错图了,应该是下面这张↓↓↓

也就是说,我们需要将上面的“站起-蹲下”相应的替换为“屈腿-伸腿”,以此来实现重心的变化。
这样的一种荡秋千方式为什么被称为“参变共振”呢?是因为我们系统中并没有外界驱动,我们只是通过周期性的改变重心,或者说是单摆的摆长,就实现了越荡越高的效果,也就是说起振是通过摆长这个参数的变化来实现的。这里我们需要注意一点,那就是不管是“蹲→起→蹲”,还是“屈→伸→屈”,在每一个秋千摆动的周期我们都需要进行两次这样的操作,也就是说我们重心变化的频率是单摆自身频率的两倍,这样才能实现参变振荡。
以上仅是对单身狗荡秋千法的定性分析,作为物理学从业者,我们能不能定量的分析一下这个过程呢?朗道笑了笑表示那自然是没问题的!

在朗道的理论物理教程第一卷《力学》卷中,有一节是关于参变振荡的,让我们一起来回忆一下:
对于一个一维的谐振子,其运动方程可一般性的表示为:

在这里的频率是含时的,不妨考虑其具有如下的形式:

其中:

也就是说该方程描述的系统的频率是周期性变化的,且频率平方的周期性变化速度大约是其自身的两倍。
众所周知,单摆在小角度振荡时,其周期与摆长的平方根成正比:

也就是说,摆长与频率的平方成反比。既然在我们的单身狗荡秋千法里,摆长的变化周期是系统本征频率的两倍,那么频率的平方自然也要以本征频率的两倍来变化啦。因此我们是可以用这个方程去描述单身狗荡秋千法的。
回到我们的方程,可以假设解的形式为:

这种假设当然不是严格精确的,实际上x还会包含更高阶的倍频项,不过他们都是h的高阶小量,所以我们可以暂时忽略。
这里我们假设相对于sin以及cos项以外,a(t)与b(t)随时间变化很慢:

将我们假设的解的形式代入到运动方程中,仅保留ε的一阶项,同时通过展波近似忽略掉以3(ω+ε/2)变化的快变项,可以得到:

注意在推导过程中我们用到了如下面这样的三角函数关系式:

上述等式若要时刻成立,sin项与cos项前面的系数必然为零,同时由于我们期望得到起振的解,因此可假设振幅是指数变化的:

最终可联立方程组如下:

方程组有解的条件为其行列式等于零,因此:

若要起振,s需为实数,因此:

回顾一开始我们考虑频率的变化为:

因此,只有当频率平方的变化频率大约是本征频率的两倍时,才会发生参变振荡,而这与我们之前对单身狗荡秋千的定性分析不谋而合!
故事讲到这里,可能有不少小伙伴要问了,这和标题里的量子计算有啥关系,难道我又被中二所骗了?(。•ˇ‸ˇ•。) 不不不,接下来才是重头戏!
02
量子计算机
量子计算的概念近几年非常火热,想必大家都有听说过。在某些特定问题的求解上,相比于经典计算机,量子计算机能够实现指数加速。比如对于我们目前最常见的RSA加密算法来说,如果采用2048位的话,哪怕是超算也需要将近10亿年的时间才能破解,但对于量子计算机来说或许只需要几分钟的时间。
那么怎样才能造出一台算力如此强大的量子计算机呢?目前进展最快的超导量子计算背后的原理其实是“电路量子电动力学(Circuit-QED)”,与光与原子相互作用的“腔量子电动力学(Cavity-QED)”相似,这里只是将真实的原子替换为了以约瑟夫森结电路为核心器件的“人造原子”,把光学谐振腔替换为了LC谐振电路。这样的系统有很大的优势,比如量子比特和测量系统的谐振腔更容易耦合,可以通过微加工的方式来实现比特的扩展等。
但是在超导量子计算的谐振腔里存在的是微波光子,典型的频率在10GHz量级。日常生活中最常见的可见光波长范围在400到760纳米之间,也就意味着其频率范围处于395~750THz的级别,从能量上来讲差不多是微波光子的十万倍。正在看文章的你,每秒要接受来自手机屏幕的百亿亿量级的可见光光子才能够获取信息。而一个典型的超导谐振腔内的微波光子数只在10这个量级。可想而知,在超导量子计算机中想要获取量子比特的信息是多么困难。
正因如此,为了测到量子比特的状态,我们需要对极其微弱的信号进行放大,总的增益需要达到100dB(也就是100亿倍!),单靠一个放大器是很难实现这一点的,往往需要级联多级放大器。但这又涉及到噪声的问题,每一级放大器引入的噪声都会随着信号被后面的放大器一起放大,如果不控制好放大器自身引入的噪声,最终的信噪比将惨不忍睹,这就使得最前端的放大器尤其重要。讲到这里本文的c位终于可以出道了,那就是“约瑟夫森参量放大器”。
03
约瑟夫森参量放大器
在讲约瑟夫森参量放大器之前,我们有必要先介绍一下约瑟夫森结,它的结构很简单,就是两个超导体中间以绝缘层隔开(如下图所示),就像三明治一样。

然而,如此简单的结构却蕴藏着极其丰富的物理现象与巨大的实用价值,它不仅给22岁的博士生布赖恩·约瑟夫森带来了1973年的诺贝尔物理学奖(注:约瑟夫森于1962年提出约瑟夫森结的理论,11年后获奖),还成为了现如今谷歌,IBM等公司正如火如荼研究的量子计算机的核心器件。那么它是怎么做到的呢?
大家知道超导体之所以能够实现零电阻,是因为超导体中的电子可以两两抱团组成库珀对儿,抱团后的电子就可以无视各种散射,一路畅通无阻了。但是一旦离开了超导体,遇到绝缘层的话该怎么办呢?在量子力学中,面对一堵墙(势垒),无论它多么高、多么坚固,电子都有一定的几率可以穿墙而过。那么面对绝缘层这堵墙,库珀对当然也是有几率隧穿过去的。但是这堵墙毕竟号称绝缘层,库珀对武功再强,总是要给人家一些面子的对不对。于是两相权衡下,库珀对可以通过,但必须受到限制。这种限制的具体形式则可以说明约瑟夫森结具有非线性的特性。
而约瑟夫森结的神奇之处便在于非线性,利用它的非线性特性人们可以构造能级间距变化的非谐振电路,就像“人造原子”一样,我们可以分辨出它的基态与激发态,因此它可以作为一个超导量子比特,占到量子计算机里的c位。也正是由于它的非线性特性,以约瑟夫森结为核心的微波电路的振荡频率可以周期性的变化。所以类似于荡秋千时摆长的周期性变化能使我们越荡越高一样,频率的周期性变化使得约瑟夫森结可以将电信号不断放大,实现参量放大的效果。下面我们将定量地介绍一下约瑟夫森结的非线性特性以及怎样通过这种非线性来实现参变振荡。
前方高能预警:一大波公式即将来袭,非战斗人员请直接撤退至文末看重点!约瑟夫森结的电流与电压满足下面两个约瑟夫森方程:
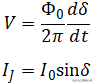
其中δ是两侧超导体的相位差,Φ0是常数,I0是约瑟夫森结允许通过的最大电流,即临界电流。结合上面两个式子可以得到:

结合电感的定义我们可以得到约瑟夫森结的电感为:

随着电流的变化,相位差δ会变化,因此约瑟夫森结的电感并不是定值,而是变化的,我们将其称为非线性电感,这便是约瑟夫森结的非线性特性。

那么怎样利用非线性特性实现参变振荡呢?且看下面的讲解:
我们考虑一个传输线与约瑟夫森结连接的模型,如上图所示。其中约瑟夫森结被等效成了右侧一个非线性电感与电容的并联,根据前面的约瑟夫森方程,它的电流大小分别为:

而在左侧的传输线上,我们需要给一个泵浦信号以及一个要放大的小信号,根据电报方程得到的边界条件,在z=0处的电流可以表示为:

在z=0的地方,两侧电流大小应相等,整理方程可得:

其中sin项已被泰勒展开至三阶项,成为方程中的非线性部分。为了求解这个方程,我们可以先忽略右侧的小输入信号,只考虑泵浦信号的影响,则方程变为:

假定剩余部分解的形式为:

这种假设显然不是精确的,但我们可以将其作为0阶近似,通过迭代的方式一步步趋近真实的解,思路类似于解非线性的Duffing方程。不过在这里我们只想要说明参量放大的物理过程,因此先将就着用这个0阶的解。
对于等式右边需要放大的小信号,我们可以将它的影响当作一个小的微扰,即:

将它代入到等式中去,只保留δS的一阶项,我们可以得到:

其中频率的表达式如下:

对比前面荡秋千那部分朗道书中的公式:

可以发现两个方程形式上是一致的,频率的平方都有着周期性的变化,因此我们的约瑟夫森结也能够像荡秋千一样参变振荡从而实现信号放大的效果。在描述约瑟夫森结的方程中多了一个微弱的输入信号和对时间一阶导的阻尼项,前者我们可以忽略不计,而后者也只会影响到约瑟夫森参量放大器的增益带宽。参变振荡的物理本质并不会有所改变。
在之前荡秋千时我们曾讲过参变振荡的频率平方的变化频率需要是系统本征频率的二倍。在这种约瑟夫森参量放大器中,我们可以看到频率平方的变化频率为泵浦频率的两倍,也就是说若想实现参量放大,需要满足泵浦信号与系统的本征频率接近,即:

04
划重点,坚持看到这里的同学真的很棒!
当我们孤身一人荡秋千时,可以通过周期性地改变自身重心使得单摆摆长周期性振荡,从而实现参变振荡,越荡越高。在量子计算机里这个过程是类似的,只不过这里我们是通过约瑟夫森结的非线性特性来让频率这个参量周期性变化,从而实现参变振荡,放大我们需要的信号。而且两者共通的一点是,参量的变化频率需要在系统本征频率的两倍附近才能够实现起振的作用。
随着科技的发展,人们研究的内容也越来越深入,在未来必然会出现更多类似于量子计算这样需要对极微弱信号进行低噪声放大的需求(目前做暗物质研究的科学家们已经开始关注约瑟夫森结参量放大器了)。不知看完这篇文章后,你是否已经有了对参量放大器的基本印象呢?
(篇幅所限,本文只是介绍了约瑟夫森参量放大器的冰山一角。关于参量放大器的参量过程,信号增益,带宽,噪声抑制,动态范围以及现如今人们为了提高这些性能进行的诸多改进。)
备注:来源网络,侵删~~
